
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

【答案】(1)证明见解析;(2)6.
【解析】试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
试题解析:(1)证明:在□ABCD中,AD∥BC,AB∥CD,∴ ∠ADF=∠CED,∠B+∠C=180°,∴ ∠C=180°-∠B.
∵ ∠AFE+∠AFD=180°,∠AFE=∠B,∴ ∠AFD=180°-∠B,∴ ∠AFD=∠C,∴ △ADF∽△DEC;
(2)在□ABCD中,CD=AB=8,∵ △ADF∽△DEC, ∴ ![]() ,∴
,∴ ![]() ,∴ DE=12.
,∴ DE=12.
∵ AD∥BC,AE⊥BC,∴ AE⊥AD.在Rt△AED中,![]() .
.


科目:初中数学 来源: 题型:
【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
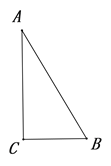
已知:如图,在![]() △
△![]() 中,
中, ![]() °,
°,![]() °.
°.
求证: ![]() .
.
证明:
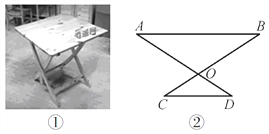
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度![]() .
.
求:桌面与地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:

(1)该镇本次统计的小微企业总个数是 ,扇形统计图中B类所对应扇形圆心角的度数为 度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, AD平分∠BAC交BC于D,DE⊥AB于E
求证:(1)△ACD≌△AED;(2)若AB=6,求△DEB的周长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的排水管每小时排水8m3,6小时可将满池水全部排空.
(1)蓄水池的容积是____________ m3;
(2)如果增加排水管,使每小时排水量达到Q(m3),那么将满池水排空所需时间为t(小时),则Q与t之间关系式为____________;
(3)如果准备在5小时内将满池水排空,那么每小时的排水量至少为____________ m3/小时;
(4)已知排水管最多为每小时12m3,则至少____________小时可将满池水全部排空.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
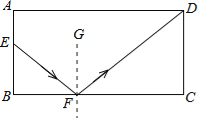
(1)求证:△BEF∽△CDF;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).

(1)在如图的平面直角坐标系中画出△ABC关于x轴对称的△A'B'C',并分别写出A′,B′,C′的坐标;
(2)将△ABC向左平移5个单位,请画出平移后的△A″B″C″,并写出△A″B″C″各个顶点的坐标;
(3)求出(2)中的△ABC在平移过程中所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___________,SAS
易证△AFG≌___________△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°.点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______________∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区便民超市为了了解顾客的消费情况,在该小区居民中进行调查,询问每户人家每周到超市的次数,下图是根据调查结果绘制的,请问:
(1)这种统计图通常被称为什么统计图?(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市?(4)请将这幅图改为扇形统计图.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com