
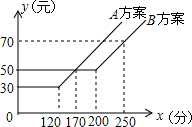
 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:分析 当B方案为50元时,A方案如果是40元或者60元,才能使两种方案通讯费用相差10元,先求两种方案的函数解析式,再求对应的时间
解答 解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x-120)×[(50-30)÷(170-120)]=0.4x-18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70-50)÷(250-200)](x-200)=0.4x-30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x-18,∴x=195,
B:60=0.4x-30,∴x=225,故(3)正确;
将yA=40或60代入,得x=145分或195分,故(4)错误;
故答案为:①②③
点评 本题考查了分段函数的应用,需注意两种付费方式都是分段函数,难点是根据所给函数上的点得到两个函数的解析式,而后结合图象进行判断.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
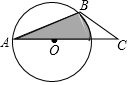 如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )
如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )| A. | 18$\sqrt{2}$+9π | B. | 9$\sqrt{2}$+4.5π | C. | 9$\sqrt{2}$+9π | D. | $\frac{9}{2}$$\sqrt{2}$+4.5π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
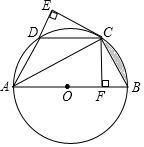 已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD于点E,且CE=CF.
已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD于点E,且CE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
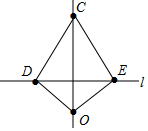 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )| A. | 到一个角两边距离相等的点在这个角的角平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 到线段两端距离相等的点在这条线段的垂直平分线上 | |
| D. | 线段垂直平分线上的点到线段两端的距离相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com