
【题目】观察、猜想、探究:
在![]() 中,
中,![]() .
.
![]() 如图
如图![]() ,当
,当![]() ,AD为
,AD为![]() 的角平分线时,求证:
的角平分线时,求证:![]() ;
;
![]() 如图
如图![]() ,当
,当![]() ,AD为
,AD为![]() 的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;
的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;
![]() 如图
如图![]() ,当AD为
,当AD为![]() 的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.

【答案】(1)见解析;(2) AB=CD+AC ,理由见解析;(3) B=CD-AC,理由见解析.
【解析】
(1)过D作DE⊥AB,交AB于点E,理由角平分线性质得到ED=CD,利用HL得到直角三角形AED与直角三角形ACD全等,由全等三角形的对应边相等,对应角相等,得到AE=AC,∠AED=∠ACB,由∠ACB=2∠B,利用等量代换及外角性质得到一对角相等,利用等角对等边得到BE=DE,由AB=AE+EB,等量代换即可得证;
(2)AB=CD+AC,理由为:在AB上截取AG=AC,如图2所示,由角平分线定义得到一对角相等,再由AD=AD,利用SAS得到三角形AGD与三角形ACD全等,接下来同(1)即可得证;
(3)AB=CD-AC,理由为:在AF上截取AG=AC,如图3所示,同(2)即可得证.
![]() 过D作
过D作![]() ,交AB于点E,如图1所示,
,交AB于点E,如图1所示,
![]() 为
为![]() 的平分线,
的平分线,![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
则![]() ;
;
![]() ,理由为:
,理由为:
在AB上截取![]() ,如图2所示,
,如图2所示,
![]() 为
为![]() 的平分线,
的平分线,
![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
则![]() ;
;
![]() ,理由为:
,理由为:
在AF上截取![]() ,如图3所示,
,如图3所示,
![]() 为
为![]() 的平分线,
的平分线,
![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)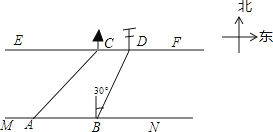
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]() = ___________;(2)
= ___________;(2)![]() =___________;(3)
=___________;(3)![]() =___________;(4)
=___________;(4)![]() =________;(5)
=________;(5)![]() __________;(6)
__________;(6)![]() =___;(7)
=___;(7)![]() _____;(8)
_____;(8)![]() =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解茂名某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题: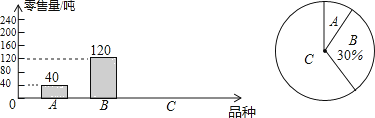
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,D1是△ABC的边AB上的一点,则图中有哪几个三角形?
(2)如图2,D1,D2是△ABC的边AB上的两点,则图中有哪几个三角形?
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有多少个三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某一周某种股票每天的收盘价(收盘价:股票每天交易结束时的价格)

(1)填表,并回答哪天收盘价最高?哪天收盘价最低?
(2)最高价与最低价相差多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com