
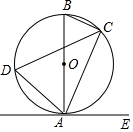
 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.分析 (1)利用同弧所对的圆周角相等确定出所求角度数即可;
(2)由AB为圆的直径,确定出所对的圆周角为直角,再由∠ABC度数求出∠BAC度数,进而求出∠BAE为直角,即可得证;
(3)连接OC,由OB=OC,且∠BOC=60°,确定出三角形OBC为等边三角形,进而求出∠AOC度数,利用弧长公式求出弧AC的长即可.
解答 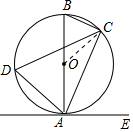 (1)解:∵∠ABC与∠D都是$\widehat{AC}$所对的圆周角,
(1)解:∵∠ABC与∠D都是$\widehat{AC}$所对的圆周角,
∴∠ABC=∠D=60°;
(2)证明:∵AB为圆O的直径,
∴∠ACB=90°,
∴∠BAC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即BA⊥AE,
∵AE经过半径OA的外端点A,
∴AE为圆O的切线;
(3)解:如图,连接OC,
∵OB=OC,∠ABC=60°,
∴△OBC为等边三角形,
∴OB=BC=2,∠BOC=60°,
∴∠AOC=120°,
则$\widehat{AC}$的长为$\frac{120π×2}{180}$=$\frac{4}{3}$π.
点评 此题考查了切线的判定,以及弧长的计算,涉及的知识有:圆周角定理,外角性质,等边三角形的判定与性质,熟练掌握定理及性质是解本题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
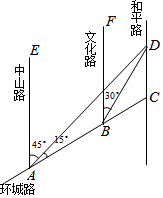 如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C,经测量,花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C,经测量,花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
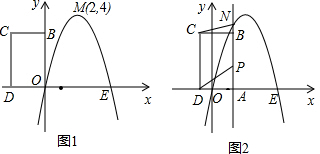
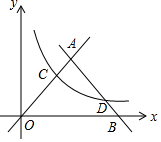 在平面直角坐标系内,双曲线:y=$\frac{k}{x}$(x>0)分别与直线OA:y=x和直线AB:y=-x+10,交于C,D两点,并且OC=3BD.
在平面直角坐标系内,双曲线:y=$\frac{k}{x}$(x>0)分别与直线OA:y=x和直线AB:y=-x+10,交于C,D两点,并且OC=3BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com