
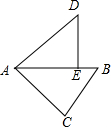
 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{5}$ |
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
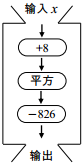 输入一组数据,按下列程序进行计算,输出结果如表:
输入一组数据,按下列程序进行计算,输出结果如表:| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
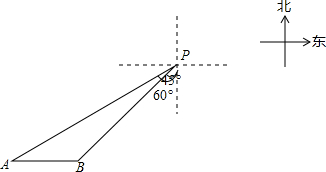 一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )| A. | 白 | B. | 红 | C. | 黄 | D. | 黑 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com