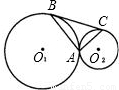
分析:(1)过点A作两圆的内公切线交BC于点O,再利用切线的性质,证明OA=OB=OC即可;
(2)连续OO
1、OO
2与AB、AC分别交于点E、F,先利用切线的性质证明四边形OEAF是矩形;
再利用三角形的形似、直角三角形的特点和三角函数求出
的值.
解答: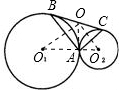
(1)证明:过点A作两圆的内公切线交BC于点O.
∵OA、OB是⊙O
1的切线,
∴OA=OB.
同理OA=OC,
∴OA=OB=OC.
于是△BAC是直角三角形,∠BAC=90°,
所以AB⊥AC.
(2)解:连接OO
1、OO
2与AB、AC分别交于点E、F.
∵OA、OB是⊙O
1的切线.
∴OO
1⊥AB,
同理OO
2⊥AC.
根据(1)的结论AB⊥AC,可知四边形OEAF是矩形,有∠EOF=90°.
连接O
1O
2,有OA⊥O
1O
2.在Rt△O
1OO
2中,有Rt△O
1AO∽Rt△OAO
2,
∴
=,
于是OA
2=O
1A•O
2A=r
1•r
2=2r
22,
∴OA=
r
2,
又∵∠ACB是⊙O
2的弦切角,
∴∠ACB=∠AO
2O.
在Rt△OAO
2中,tan∠AO
2O=
=,
∴
=tan∠ACB=tan∠AO
2O=
.
点评:本题综合考查了直线与圆、圆与圆的位置关系,全等三角形的判定、图形的平移变换等多个知识点.

 已知,如图⊙O1与⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点.
已知,如图⊙O1与⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点. (1)证明:过点A作两圆的内公切线交BC于点O.
(1)证明:过点A作两圆的内公切线交BC于点O.

 已知:如图⊙O1与⊙O2相交于A、B,P是⊙O1上一点,连接PA、PB并延长,分别交⊙O2于C、D,点E是
已知:如图⊙O1与⊙O2相交于A、B,P是⊙O1上一点,连接PA、PB并延长,分别交⊙O2于C、D,点E是
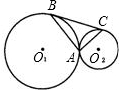 已知,如图⊙O1与⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点.
已知,如图⊙O1与⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点. 的值.
的值. 的值.
的值.
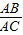 的值.
的值.