
【题目】如图,一个长方形运动场被分隔成ABABC共5个区,A区是边长为a m的正方形,C区是4个边长为b m的小正方形组成的正方形.

(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40 m,b=20 m,求整个长方形运动场的面积.
【答案】(1) (a+2b+a—2b)×2,4a ;(2)4a +2(a+2b)+2(a—2b),8a;(3) 4800 m2
【解析】
(1)利用图形得出区域B的长和宽,即可得出答案;
(2)利用图形得出整个长方形的长和宽,即可得出答案;
(3)借助(2)求出的长和宽,利用面积公式计算即可得出答案.
解:(1)由图可知:B区长方形的长是(a+b)m,宽是(a-b)m
则B区长方形的周长=(a+2b+a-2b)×2=4a(m)
(2)由图可知:整个长方形的长是(a+b+a)m,宽是(a+a-b)m
则整个长方形的周长=4a+2(a+2b)+2(a-2b)=8a (m)
(3)S=(2a-2b)×﹙2a+2b﹚=4 a2- 4b2 (m2)
当a=40,b=20时,原式=4 ×402- 4×202=4800 (m2)
答:整个长方形运动场的面积为4800 m2


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
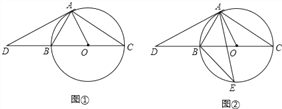
【题目】已知BC是⊙O的直径,AD是⊙O的切线,切点为A,AD交CB的延长线于点D,连接AB,AO.
(1)如图①,求证:∠OAC=∠DAB;
(2)如图②,AD=AC,若E是⊙O上一点,求∠E的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为![]() 的矩形纸板
的矩形纸板![]() ,如图
,如图![]() ,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面
,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面![]() 为矩形,如图
为矩形,如图![]() ,设小正方形的边长为
,设小正方形的边长为![]() 厘米.、
厘米.、
(1)若矩形纸板的一个边长为![]() .
.
①当纸盒的底面积为![]() 时,求
时,求![]() 的值;
的值;
②求纸盒的侧面积的最大值;
(2)当![]() ,且侧面积与底面积之比为
,且侧面积与底面积之比为![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图
(1)如图,平面上有五个点A,B,C,D,E. 按下列要求画出图形.
①连接BD;
②画直线AC交BD于点M;
③过点A作线段AP⊥BD于点P;
④请在直线AC上确定一点N,使B,E两点到点N的距离之和最小(保留作图痕迹).
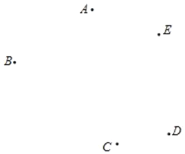
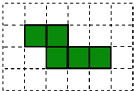
(2)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.注意:只需添加一个符合要求的正方形,并用阴影表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
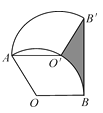
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
+11 | +10 | ﹣17 | +18 | ﹣12 |
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com