
分析 (1)若每天生产的甲种零件数不少于乙种零件数,则可以列出不等式5x≥4(20-x),得出x的取值范围,从而可以得到甲种零件最少人数;
(2)因为甲种零件可获利16元,每加工一个乙种零件可获利24元,而x人加工甲种零件,其余的加工乙种零件,每人每天可平均加工甲种零件5个或者乙种零件4个,从而可知总利润y与x的函数解析式y=16×5x+24×4(29-x)解答即可.
解答 解:(1)由题意可知:
5x≥4(20-x),
∴x≥$\frac{80}{9}$,
因此最少8人;
(2)从题意可知总利润
y=16×5x+24×4(20-x)=-16x+1920,
所以这个车间每天获得的利润y(元)与安排生产甲种零件的工人数x(人)之间的函数解析式为y=-16x+1920;
因为k=-16<0,所以y=-16x+1920是减函数,故该车间每天最多可获利润是1920元.
点评 此题考查一次函数问题,做本题时一定要读懂题意之后才开始做题,把握题中所给信息找出其中的关系然后才能正确的解答.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
| Xxx居民电费专用发票 | |
| 计费期限:一个月 | |
| 用电量(度) | 电价(元/度) |
| 阶梯一:190 | 0.53 |
| 阶梯二:190-290(超出部分) | 0.58 |
| 本月实用金额:106.5(元) | (大写)壹佰零陆元伍角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
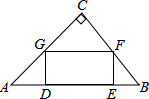 如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.
如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com