
 ,则下底BC的长为 __________.
,则下底BC的长为 __________.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源:不详 题型:解答题
 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,连接
,连接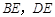 ,其中
,其中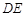 交直线
交直线 于点
于点 .
. ,求
,求 的度数;
的度数; ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.有两组对边分别平行的四边形是平行四边形 |
| B.平行四边形的对角线互相平分 |
| C.平行四边形的对角互补,邻角相等 |
| D.平行四边形的对边平行且相等 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.15°或30° | B.30°或45° |
| C.45°或60° | D.30°或60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com