
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.

【答案】4或64
【解析】
分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
如图1.
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°.
∵∠AD′B=90°,∴B、D′、E三点共线.
又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=34.
∵BD′=![]() =
=![]() =30,∴DE=D′E=34﹣30=4;
=30,∴DE=D′E=34﹣30=4;

如图2.
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″.在△ABD″和△BEC中, ,∴△ABD″≌△BEC,∴BE=AB=34,∴DE=D″E=34+30=64.
,∴△ABD″≌△BEC,∴BE=AB=34,∴DE=D″E=34+30=64.
综上所述:DE=4或64.

故答案为:4或64.


科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
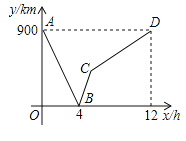
(1)甲、乙两地之间的距离为 千米;图中点B的实际意义是 ;
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时(h)”,某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;D组:t≥1.5h.
请根据上述信息解答下列问题
(1)补全条形统计图;
(2)某市约有25000名初中学生,请你结合以上数据进行
①估计达到国家规定体育活动时间的人数是多少?
②如果要估算本市初中生每天在校体育活动时间是多少,你认为选择众数、中位数和平均数三个量中的哪个更合适?

查看答案和解析>>
科目:初中数学 来源: 题型:
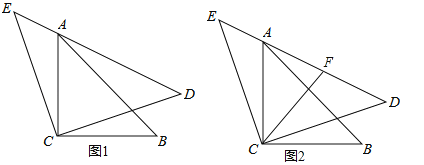
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=![]() ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
小明发现,可以设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
利用方程组可以解决.
请回答:
另一个因式为 ,m的值为 ;
参考小明的方法,解决下面的问题:
已知二次三项式2x2+3x﹣k有一个因式是(x﹣4),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;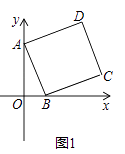
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com