练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算${（-\;\frac{1}{2}\;）^0}$的结果是（　　）
    A．-1B．$-\frac{1}{2}$C．0D．1

    分析 根据零指数幂直接计算即可．

    解答 解：${（-\;\frac{1}{2}\;）^0}$=1．
    故选D．

    点评 此题是零指数幂的运算，熟记零指数幂的计算结果是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

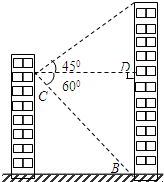    9．小明家所在居民楼的对面有一座大厦AB，AB=80米．为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为45°，大厦底部B的俯角为60°．求小明家所在居民楼与大厦的距离CD的长度．计算结果保留根号．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．（1）如图1，AC=DC，BC=EC，∠ACD=∠BCE，求证：∠A=∠D．
    （2）如图2，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，求∠ADP的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

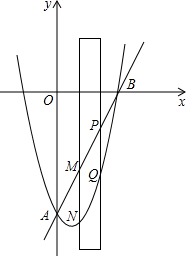    8．如图，抛物线与直线y=2x-8交于A，B两点，有一直尺平行于y轴移动，直尺两长边所在直线AB和抛物线截得两线段NM、PQ，点P、M在直线AB上且PM=$\sqrt{5}$，设M点的横坐标为m（0＜m＜4）．
    （1）求抛物线的函数解析式．
    （2）当m为何值时，以M、N、P、Q为顶点的四边形是平行四边形？请说明理由；
    （3）在抛物线上的对称轴上是否存在点D使得点D到直线AB和到x轴的距离相等？若存在，请直接写出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

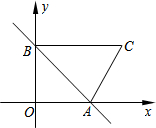    15．已知一次函数y=-x+3的图象与x轴交于点A、与y轴交于点B，BC∥x轴，且∠ACB的正切值为3．
    （1）求点A、B、C的坐标；
    （2）如果二次函数图象经过A、B、C三点，试求该抛物线的解析式及顶点M的坐标；
    （3）如果在y轴上有一点D，使得△ABD与△ABC相似，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列说法正确的是（　　）
    A．“抛掷一枚硬币，正面向上”是不可能事件
    B．一组数据2，3，4，5，5，2，4，2，2的中位数是3
    C．若甲、乙两组数据的方差分别为S甲2=1.2、S乙2=2.3，则乙组数据比甲组数据稳定
    D．掷一枚骰子，偶数点向上的概率为$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．善于思考的小明在解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{4x+11y=5②}\end{array}\right.$时，采用了一种“整体代换”的解法：
    解：将方程②变形：4x+10y+y=5，即2（2x+5y）+y=5③
        把方程①代入③得：2×3+y=5，∴y=-1
        把y=-1代入①得x=4，∴方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$．
    请你解决以下问题：
    （1）模仿小明的“整体代换”法解方程组$\left\{\begin{array}{l}{2x-y=1①}\\{6x-2y=6②}\end{array}\right.$；
    （2）已知x，y满足方程组$\left\{\begin{array}{l}{2{x}^{2}-xy+18{y}^{2}=33①}\\{3{x}^{2}+2xy+27{y}^{2}=60②}\end{array}\right.$
    ①求x2+9y2的值；
    ②求x+3y的值．[参考公式（a+b）2=a2+2ab+b2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．当$\frac{\sqrt{2x+1}}{x-1}$有意义时，x的取值范围是x≥-$\frac{1}{2}$且x≠1，
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

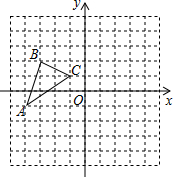    10．如图所示，在平面直角坐标系中，平移三角形ABC，使A的对应点A1的坐标为（1，-3），B的对应点为B1，C的对应点为C1．
    （1）在图中画出平移后的三角形A1B1C1；
    （2）若三角形ABC内有一点P（a，b），经平移后对应点为P1，用a，b表示P1的坐标；
    （3）求出三角形ABC的面积．

    查看答案和解析>>

    同步练习册答案