
【题目】如图,长方形![]() 中
中![]() ∥
∥![]() ,边
,边![]() ,
,![]() .将此长方形沿
.将此长方形沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 处.
处.
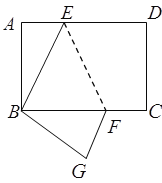
(1)试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求![]() 的面积.
的面积.
【答案】(1)![]() 是等腰三角形;(2)10
是等腰三角形;(2)10
【解析】
试题(1)根据翻折不变性和平行线的性质得到两个相等的角,根据等角对等边即可判断△BEF是等腰三角形;
(2)根据翻折的性质可得BE=DE,BG=CD,∠EBG=∠ADC=90°,设BE=DE=x,表示出AE=8-x,然后在Rt△ABE中,利用勾股定理列出方程求出x的值,即为BE的值,再根据同角的余角相等求出∠ABE=∠GBF,然后利用“角边角”证明△ABE和△GBF全等,根据全等三角形对应边相等可得BF=BE,再根据三角形的面积公式列式计算即可得解.
试题解析:解:(1)△BEF是等腰三角形.
∵ED∥FC,
∴∠DEF=∠BFE,
根据翻折不变性得到∠DEF=∠BEF,
故∠BEF=∠BFE.
∴BE=BF.
△BEF是等腰三角形;
(2)∵矩形ABCD沿EF折叠点B与点D重合,
∴BE=DE,BG=CD,∠EBG=∠ADC=90°,∠G=∠C=90°,
∵AB=CD,
∴AB=BG,
设BE=DE=x,则AE=AB-DE=8-x,
在Rt△ABE中,AB2+AE2=BE2,
即42+2=x2,
解得x=5,
∴BE=5,
∵∠ABE+∠EBF=∠ABC=90°,
∠GBF+∠EBF=∠EBG=90°,
∴∠ABE=∠GBF,
在△ABE和△MBF中,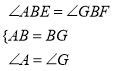
∴△ABE≌△GBF(ASA),
∴BF=BE=5,
∴△EBF的面积=![]() ×5×4=10.
×5×4=10.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
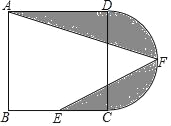
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目:初中数学 来源: 题型:
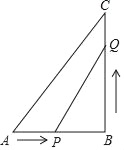
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)在(1)中,△PQB的面积能否等于8cm2?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
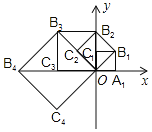
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推……则正方形OB2019B2020C2020的顶点B2020的坐标是 _____.
查看答案和解析>>
科目:初中数学 来源: 题型:
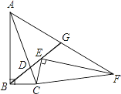
【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为________.
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
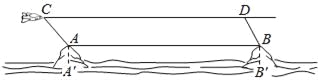
【题目】如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AC,AB上,BD与CE相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABD≌△ACE的是( )

A.AD=AEB.AB=ACC.BD=CED.∠ADB=∠AEC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com