
分析 (1)计算判别式的值得到△=(3m+1)2,然后根据非负数的意义得到△≥0,从而根据判别式的意义可判断无论m取任何实数时,原方程总有两个实数根;
(2)利用求根公式法解关于x的一元二次方程 x1=m,x2=4m+1,则当$\frac{x_1}{x_2}=\frac{m}{4m+1}$时,m=0;当$\frac{x_2}{x_1}=\frac{4m+1}{m}$,利用整除性得到m=±1.
解答 (1)证明:△=[-(5m+1)]2-4×1×(4m2+m)
=9m2+6m+1
=(3m+1)2,
∵无论m取任何实数时,
∴(3m+1)2≥0,
∴无论m取任何实数时,原方程总有两个实数根;
(2)解:解关于x的一元二次方程x2-(5m+1)x+4m2+m=0得 x1=m,x2=4m+1,
∴当$\frac{x_1}{x_2}=\frac{m}{4m+1}$时,m=0;
当$\frac{x_2}{x_1}=\frac{4m+1}{m}$时,$\frac{4m+1}{m}=4+\frac{1}{m}$,所以m=±1
综上所述m=0或m=±1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
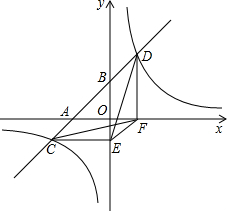 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数$y=\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数$y=\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
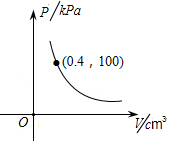 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Kpa)是气体体积V(cm3)的反比例函数,其图象如图所示,当气球内气压大于120Kpa时,气球将爆炸,为了安全,该气球内气体体积V(cm3)的取值范围是V≥$\frac{1}{3}$.
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Kpa)是气体体积V(cm3)的反比例函数,其图象如图所示,当气球内气压大于120Kpa时,气球将爆炸,为了安全,该气球内气体体积V(cm3)的取值范围是V≥$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com