
已知抛物线y=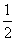 x2+x+c与x轴没有交点.
x2+x+c与x轴没有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限,并说明理由.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(1)求证: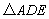 ≌
≌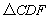 .
.
(2)把 向左平移,使
向左平移,使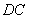 与
与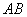 重合,得
重合,得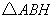 ,
,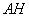 交
交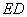 于点
于点 .请判断AH与ED的位置关系,并说明理由.
.请判断AH与ED的位置关系,并说明理由.
(3)求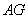 的长.
的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形的周长是C cm,面积为S cm2.
(1)求S与C之间的函数关系式;
(2)画出图象;
(3)根据图象,求出S=1 cm2时,正方形的周长;
(4)根据图象求出C取何值时,S≥4 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图2219,A(-1,0),B(2,-3)两点都在一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象上.
(1)求m的值和二次函数的解析式;
(2)请直接写出当y1>y2时,自变量x的取值范围.

图2219
查看答案和解析>>
科目:初中数学 来源: 题型:
小李想用篱笆围成一个周长为60米的矩形场地,设矩形面积为S(单位:平方米),一边长为x(单位:米).
(1)S与x之间的函数关系式为____________,自变量x的取值范围为____________;
(2)当x=________时,矩形场地面积S最大?最大面积是________平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
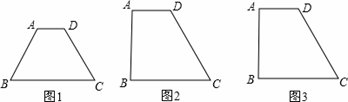
某同学在研究四边形的相关性质时发现,在不改变面积的条件下,一般梯形很难转化为菱形,但有些特殊的梯形通过分割可以转化为菱形.例如以下的等腰梯形就可以转化为菱形(如图1),已知在等腰梯形ABCD中,AD∥BC,AD=10,CD=20,∠C=60°.
(1)求梯形ABCD的面积;
(2)如果将该梯形分割成几块,然 后可以重新拼成菱形,试画出变化后的图形(在图1中画出,图形的对应部分标明相同的编号);
后可以重新拼成菱形,试画出变化后的图形(在图1中画出,图形的对应部分标明相同的编号);
(3)在完成上述任务后,他又试着将梯形的形状变为直角梯形(如图2),其它条件不变,将梯形分成几块.
 ①他能拼成一个菱形吗?如果能,请在图2中
①他能拼成一个菱形吗?如果能,请在图2中 画出相应的图形;
画出相应的图形;
②他能拼成一个正六边形吗?如果能,请在图3中画出相应的图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com