练习册

  • 练习册
  • 试题
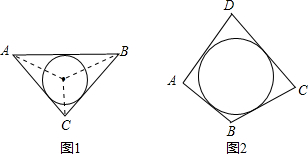    精英家教网 > 初中数学 > 题目详情
    如图，利用四边形的不稳定性改变矩形ABCD的形状，得到?A1BCD1，若?A1BCD1的面积是矩形ABCD面积的一半，则∠ABA1的度数是（ ）

    A．15°
    B．30°
    C．45°
    D．60°
    【答案】分析：过A1作A1H⊥BC于H，根据?A1BCD1的面积是矩形ABCD面积的一半，求出A1H=A1B，根据含30度角的直角三角形性质求出∠A1BH=30°即可．
    解答：
    解：过A1作A1H⊥BC于H，
    ∵?A1BCD1的面积是矩形ABCD面积的一半，
    ∴AB×BC=2BC×A1H，
    ∴A1H=A1B，
    ∴∠A1BH=30°，
    ∴∠ABA1=90°-30°=60°，
    故选D．
    点评：本题考查了含30度角的直角三角形性质，矩形的性质和平行四边形的性质等知识点的应用，关键是求出A1H=A1B，用的数学数学是转化思想，即把实际问题转化成数学问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    精英家教网阅读材料：如图1，△ABC的周长为l，面积为S，内切圆O的半径为r，探究r与S、l之间的关系．连接OA，OB，OC∵S=S△OAB+S△OBC+S△OCA
    又∵S△OAB=
    1
    2
    AB•r    ，S△OBC=
    1
    2
    BC•r    ，S△OCA=
    1
    2
    CA•r
    ∴S=
    1
    2
    AB•r+
    1
    2
    BC•r+
    1
    2
    CA•r=
    1
    2
    l•r
    ∴r=
    2S
    l

    解决问题：
    （1）利用探究的结论，计算边长分别为5，12，13的三角形内切圆半径；
    （2）若四边形ABCD存在内切圆（与各边都相切的圆），如图2且面积为S，各边长分别为a，b，c，d，试推导四边形的内切圆半径公式；
    （3）若一个n边形（n为不小于3的整数）存在内切圆，且面积为S，各边长分别为a1，a2，a3，…，an，合理猜想其内切圆半径公式（不需说明理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

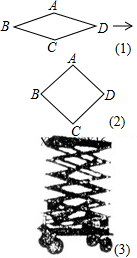    （2011•朝阳）如图（3）是利用四边形的不稳定性制造的一个移动升降装修平台，其基本图形是菱形，主体部分相当于由6个菱形相互连接而成，通过改变菱形的角度，从而可改变装修平台高度．
    （1）如图（1）是一个基本图形，已知AB=1米，当∠ABC为30°时，求AC的长及此时整个装修平台的高度（装修平台的基脚高度忽略不计）；
    （2）当∠ABC从30°变为90°（如图（2）是一个基本图形变化后的图形）时，求整个装修平台升高了多少米．
    [结果精确到0.1米，参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，
    		2
    ≈1.41]．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省朝阳市2011年初中毕业升学考试数学试卷 题型：044

    如图是利用四边形的不稳定性制造的一个移动升降装修平台，其基本图形是菱形，主体部分相当于由6个菱形相互连接而成，通过改变菱形的角度，从而可改变装修平台高度．

    (1)如图是一个基本图形，已知AB＝1米，当∠ABC为30°时，求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计)；

    (2)当∠ABC从30°变为90°(如图是一个基本图形变化后的图形)时，求整个装修平台升高了多少米．

    [结果精确到0.1米，参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，≈1.41]

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省太仓市七年级期中考试数学卷（带解析） 题型：解答题

    探究与发现：
    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．

    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
    已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

    探究三：若将△ADC改为任意四边形ABCD呢？
    已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

    探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？
    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：_______________________________．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省太仓市七年级下学期期中考试数学试卷（带解析） 题型：解答题

    探究与发现：
    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？
    已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，
    试探究∠A与∠FDC+∠ECD的数量关系．

    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
    已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．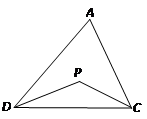

    探究三：若将△ADC改为任意四边形ABCD呢？
    已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

    探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？
    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系： _______________________________．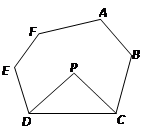

    查看答案和解析>>

    同步练习册答案