练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
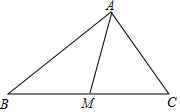
    7．如图，在△ABC中，AM是BC边上的中线，求证：AM＜（AB+AC）．

    分析 延长AM到D，使MD=AM，连CD，证△ABM≌△DCM得AB=CD，进而在△ACD中利用三角形三边关系，证之．

    解答 证明：如图，延长AM到D，使MD=AM，连CD，

    ∵AM是BC边上的中线，
    ∴BM=CM，
    在△ABM和△DCM中，
    ∵$\left\{\begin{array}{l}{BM=CM}\\{∠BMA=∠CMD}\\{AM=DM}\end{array}\right.$，
    ∴△ABM≌△DCM（SAS），
    ∴AB=CD，
    在△ACD中，则AD＜AC+CD，
    即2AM＜AC+AB，
    ∴AM＜$\frac{1}{2}$（AB+AC）＜AB+AC．

    点评 本题主要考查了全等三角形的判定及性质以及三角形的三边关系问题，添加辅助线构建全等三角形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．如图，抛物线y=ax2+bx+c经过A（-2，0）、B（2，$\frac{16}{5}$），且抛物线过点C（0，$\frac{16}{5}$）
    （1）求抛物线的解析式；
    （2）若点P是位于直线AB上方抛物线上的一个动点，当△PAB的面积最大时，求点P的坐标；
    （3）连接BC，在抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．3月5日是学雷锋日，某校组织了以“向雷锋同志学习”为主题的小报制作比赛，评分结果只有60，70，80，90，100五种．现从中随机抽取部分作品，对其份数及成绩进行整理，制成如下两幅不完整的统计图．根据以下信息，解答下列问题：
    （1）求本次抽取了多少份作品，并补全两幅统计图；
    （2）已知该校收到参赛作品共1200份，请估计该校学生比赛成绩达到90分以上（含90分）的作品有多少份？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

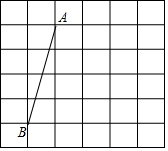    7．如图，在网格中，每个小正方形的边长均为1个单位长度，我们将小正方形的顶点叫做格点，线段AB的端点均在格点上．
    （1）将线段AB向右平移3个单位长度，得到线段A′B′，画出平移后的线段并连接AB′和A′B，两线段相交于点O；
    （2）求证：△AOB≌△B′OA′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．10月9日新浪网报道，2015年全球大米产量为4.7576亿吨，比2014年下降0.59%．某天王阿姨在超市买了10斤大米，她又打算买些小米，看过小米的价钱后，她发现，买8斤小米的总费用比买10斤大米的贵13元；买4斤小米的总费用比买10斤大米的便宜5元，则每斤小米的价钱为（　　）
    A．4.5元B．4元C．3.5元D．3元

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．化简：
    （1）-4ab+$\frac{1}{3}$b2-9ab-$\frac{1}{2}$b2
     （2）x+[-x-2（x-2）]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知等腰三角形的周长为6cm，底边长y（cm）是腰长x（cm）的函数，
    （1）写出这个函数的关系式；
    （2）求自变量x的取值范围；
    （3）画出函数图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知点A（t，1）为函数y=ax2+bx+4（a，b为常数，且a≠0）与y=x图象的交点．
    （1）求t；
    （2）若函数y=ax2+bx+4的图象与x轴只有一个交点，求a，b；
    （3）若1≤a≤2，设当$\frac{1}{2}$≤x≤2时，函数y=ax2+bx+4的最大值为m，最小值为n，求m-n的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

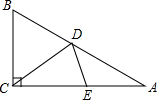    17．如图，Rt△ABC中，∠ACB=90°，∠B=60°，AB=2，点D是边AB上任意一点，点E是边AC上任意一点，连接DE、DE，则DC+DE的最小值为$\frac{3}{2}$．

    查看答案和解析>>

    同步练习册答案