
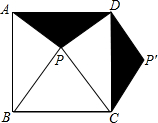
 正方形ABCD内一点P,使△PBC为等边三角形,连接PA,PD,把△PAD绕点D以逆时针方向旋转90°得△DCP?,则∠DCP?=________度.
正方形ABCD内一点P,使△PBC为等边三角形,连接PA,PD,把△PAD绕点D以逆时针方向旋转90°得△DCP?,则∠DCP?=________度. 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
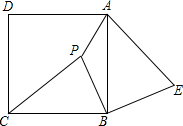 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.查看答案和解析>>
科目:初中数学 来源: 题型:
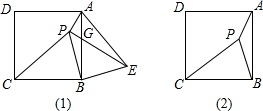 如图(1),P是正方形ABCD内一点,将△PBC绕点B按顺时针方向旋转后与△EBA重合.
如图(1),P是正方形ABCD内一点,将△PBC绕点B按顺时针方向旋转后与△EBA重合.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com