
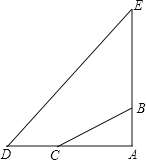
【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)
科目:初中数学 来源: 题型:
【题目】将方程3x(x﹣1)=5(x+2)化为一元二次方程的一般式,正确的是( )
A.4x2﹣4x+5=0B.3x2﹣8x﹣10=0C.4x2+4x﹣5=0D.3x2+8x+10=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.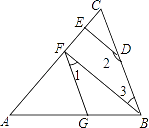
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=![]() 的图象经过D点.
的图象经过D点.
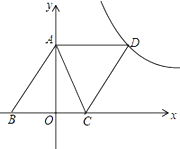
(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC= , 若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.
(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com