
分析 关键描述语是:“一部分人骑自行车先走40分钟后,其余人乘汽车出发,结果他们同时到达”;等量关系为:乘汽车同学所用的时间=骑自行车同学所用的时间-40分钟,根据等量关系列式.
解答 解:设自行车的速度为x千米/时,那么骑自行车用的时间为:$\frac{15}{x}$小时,而坐汽车用的时间为:$\frac{15}{3x}$小时;
根据骑自行车多用了40分钟即$\frac{40}{60}$小时,那么方程可表示为:$\frac{15}{3x}$=$\frac{15}{x}$-$\frac{40}{60}$.
故答案为$\frac{15}{3x}$=$\frac{15}{x}$-$\frac{40}{60}$.
点评 本题考查了由实际问题抽象出分式方程,列方程解应用题的关键步骤在于找相等关系.本题用到的等量关系为:时间=路程÷速度.注意时间单位的统一.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-$\frac{7}{4}$ | B. | k≥-$\frac{7}{4}$ 且k≠0 | C. | k≥-$\frac{7}{4}$ | D. | k>$\frac{7}{4}$ 且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
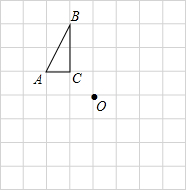 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com