

���� ��1�����ݾ��ε����ʣ��ɵ�B�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2������ƽ����AC�������������е�ֱ�ߵ�AC�ľ�����ɵ�P��ƽ�����������ߵ�Ψһ���㣬���ݽⷽ���飬�ɵ�P�����ꣻҲ��������������ʾ��PAC��������ó�������ϵʽ������ֵ��Ҳ���������P�����ꣻ
��3������BD����O��OM��BD�ڵ�M����AB�ڵ�Q��������֤����QBM=30�㣬�Ӷ��ɵõ��ӵ�Q��A���Q����O����ʱ����ͬ���Ӷ���ȷ����Q�����꣮
��� �⣺��1���ɾ���OABC������ƽ��ֱ������ϵ�У���A��3��0����C��0��3$\sqrt{3}$�����ã�
B��������3��3$\sqrt{3}$����
��B��D��������뺯������ʽ���ã�
$\left\{\begin{array}{l}{9a+3b=3\sqrt{3}}\\{36a+6b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$��
��2����ͼ1������P��ƽ����AC��ֱ�ߣ���ֱ���������߽���һ������ʱ����PAC��������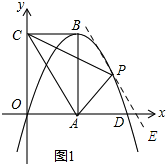 ��A��3��0����C��0��3$\sqrt{3}$����
��A��3��0����C��0��3$\sqrt{3}$����
��ֱ��AC�Ľ���ʽΪ��y=-$\sqrt{3}$x+3$\sqrt{3}$��
�����P��ֱ�߽���ʽΪy=-$\sqrt{3}$x+b������ֱ���������߽���ʽ����$\left\{\begin{array}{l}{y=-\sqrt{3}x+b}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+2\sqrt{3}x}\end{array}\right.$��
��������$\frac{\sqrt{3}}{3}$x2-3$\sqrt{3}$x+b=0��
��=81-4$\sqrt{3}$b=0��
���b=$\frac{27}{4}\sqrt{3}$��
$\frac{\sqrt{3}}{3}$x2-3$\sqrt{3}$x+$\frac{27}{4}\sqrt{3}$=0��
���x1=x2=$\frac{9}{2}$��y=-$\sqrt{3}$��$\frac{9}{2}$+$\frac{27}{4}\sqrt{3}$=$\frac{9\sqrt{3}}{4}$��
��P��������$\frac{9}{2}$��$\frac{9\sqrt{3}}{4}$����
��3����ͼ2������BD����O��OM��BD�ڵ�M����AB�ڵ�Q��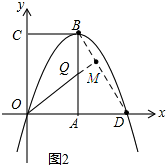 ��AD=3��AB=3$\sqrt{3}$��
��AD=3��AB=3$\sqrt{3}$��
���QBM=30�㣬
�֡�QM��BD��
���QOA=30��
��AQ=$\frac{1}{2}$OQ��
���趯����BQ�ϵ��ٶ�Ϊ1������OQ�ϵ��ٶ�Ϊ2��
�ද����OQ���˶���ʱ����ڶ�����ԭ�ٶ���AQ���˶���ʱ�䣬
���ӵ�B�˶���Q�����˶���O���൱����ԭ�ٶȴ�B�˶���A��ʱ�䣬
�൱OM��BDʱ����AB��Q����ʱ�ĵ�Q��������ĵ㣬
tan30��=$\frac{AQ}{AO}$=$\frac{\sqrt{3}}{3}$��
��$\frac{AQ}{3}$=$\frac{\sqrt{3}}{3}$��
��AQ=$\sqrt{3}$��
��Q��3��$\sqrt{3}$����
���� �����Ƕ��κ������ۺ��⣬���������ô���ϵ���������Ľ���ʽ�����dz������ͣ�Ҫ�������գ���������������ֵ�������꣬����һ����ת��Ϊ���÷�����������⣬Ҳ�������ö��κ����Ķ������꣨��ֵ�����������ꣻ����Ѻ����ͼ����л��Ľ����һ�𣬿��Ƽ���ʵ�Ƚϸ��ӣ�Ҫ�����������⣬Ҫ��ʱ�����Сֵ����ת��Ϊ�߶ε���Сֵ��������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ�γ�Ϊ30m�����Χ��һ�߿�ǽ�ľ��β���ǽ��Ϊ18m������Ŀ�ABΪxm�����ΪSm2��
��ͼ����һ�γ�Ϊ30m�����Χ��һ�߿�ǽ�ľ��β���ǽ��Ϊ18m������Ŀ�ABΪxm�����ΪSm2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ�濿ǽ�Ŀյ����ó�Ϊ24����ʣ�Χ���м���ж�����ʵij����λ��ԣ��軨�ԵĿ�ABΪx�ף����ΪSƽ���ף�
��ͼ����һ�濿ǽ�Ŀյ����ó�Ϊ24����ʣ�Χ���м���ж�����ʵij����λ��ԣ��軨�ԵĿ�ABΪx�ף����ΪSƽ���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
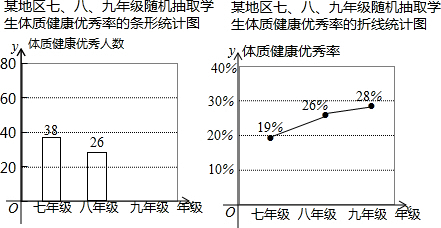
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com