
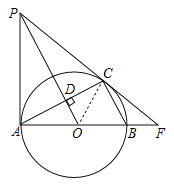
【题目】如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与
OD的延长线交于点P,PC、AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.

【答案】(1)证明见解析(2)5![]()
【解析】
(1)连接OC,可以证得△OAP≌△OCP,利用全等三角形的对应角相等,以及切线的性质定理可以得到:∠OCP=90°,即OC⊥PC,即可证得;
(2)先证△OBC是等边三角形得∠COB=60°,再由(1)中所证切线可得∠OCF=90°,结合半径OC=5可得答案.
(1)连接OC.
∵OD⊥AC,OD经过圆心O,∴AD=CD,∴PA=PC.
在△OAP和△OCP中,∵ ,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP.
,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP.
∵PA是半⊙O的切线,∴∠OAP=90°,∴∠OCP=90°,即OC⊥PC,∴PC是⊙O的切线.
(2)∵OB=OC,∠OBC=60°,∴△OBC是等边三角形,∴∠COB=60°.
∵AB=10,∴OC=5.
由(1)知∠OCF=90°,∴CF=OCtan∠COB=5![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.

(1)求证:△ACE≌△BCF;
(2)若∠BFE=60°,求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )

A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》,其主要突破在“五边形数”的证明上.如图为前几个“五边形数”的对应图形,请据此推断,第10个“五边形数”应该为( ),第2018个“五边形数”的奇偶性为( )

A. 145;偶数 B. 145;奇数 C. 176;偶数 D. 176;奇数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的等腰直角三角形按如图方式放置在平面直角坐标系中,OA在x轴上,已知∠COD=∠OAB=90°,OC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求k的值.
(2)把△OCD沿射线OB移动,当点D落在y=![]() 图象上时,求点D经过的路径长.
图象上时,求点D经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )

A. 10 B. 12 C. 15 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在
在![]() 轴的正半轴上,以
轴的正半轴上,以![]() 为斜边向上作等腰直角
为斜边向上作等腰直角![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 轴的正半轴运动,设运动时间为
轴的正半轴运动,设运动时间为![]() 秒,连接
秒,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子来表示
的式子来表示![]() ;
;
(3)如图3,在(2)的条件下,当点![]() 在
在![]() 的延长线上时,点
的延长线上时,点![]() 在直线
在直线![]() 的下方,且
的下方,且![]() ,
,![]() .连接
.连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com