
���Ķ�����֪ʶ��Ȼ���������������⣺
����һ��δ֪��������δ֪������ߴ�ָ����2�ķ��̣�����һԪ���η��̣��磺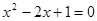 .
.
���ǰ�����һ����ʽ������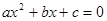 (a��b��c��ʾ��֪����
(a��b��c��ʾ��֪���� ��δ֪����a��0)�����Ľ������ǣ�
��δ֪����a��0)�����Ľ������ǣ�
�� ��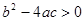 ʱ����������������ȵĽ⣻
ʱ����������������ȵĽ⣻
�� ��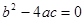 ʱ��������������ȵĽ⣨��һ���⣩��
ʱ��������������ȵĽ⣨��һ���⣩��
�� ��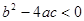 ʱ������û�н⣻
ʱ������û�н⣻
��1��һԪ���η���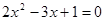 �м����⣿Ϊʲô��
�м����⣿Ϊʲô��
��2����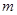 ȡ��ֵʱ������
ȡ��ֵʱ������ ��һԪ���η���
��һԪ���η���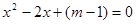 û�н⣿
û�н⣿
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�찲�պϷʹŶ���ѧ���꼶�����п�����ѧ�Ծ��������棩 ���ͣ������
���Ķ�����֪ʶ��Ȼ���������������⣺
����һ��δ֪��������δ֪������ߴ�ָ����2�ķ��̣�����һԪ���η��̣��磺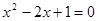 .
.
���ǰ�����һ����ʽ������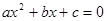 (a��b��c��ʾ��֪����
(a��b��c��ʾ��֪����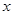 ��δ֪����a��0)�����Ľ������ǣ�
��δ֪����a��0)�����Ľ������ǣ�
�� ��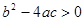 ʱ����������������ȵĽ⣻
ʱ����������������ȵĽ⣻
�� ��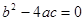 ʱ��������������ȵĽ⣨��һ���⣩��
ʱ��������������ȵĽ⣨��һ���⣩��
�� ��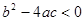 ʱ������û�н⣻
ʱ������û�н⣻
��1��һԪ���η���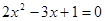 �м����⣿Ϊʲô��
�м����⣿Ϊʲô��
��2����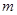 ȡ��ֵʱ������
ȡ��ֵʱ������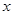 ��һԪ���η���
��һԪ���η���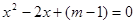 û�н⣿
û�н⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com