
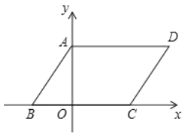
【题目】如图,在平面直角坐标系中,四边形![]() 是平行四边形,
是平行四边形,![]() ,若
,若![]() ,
,![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,且
的两个根,且![]() .
.
(1)直接写出:![]() ______,
______,![]() ______;
______;
(2)若点![]() 为
为![]() 轴正半轴上的点,且
轴正半轴上的点,且![]() ;
;
①求经过![]() ,
,![]() 两点的直线解析式;
两点的直线解析式;
②求证:![]() .
.
(3)若点![]() 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,直接写出
为顶点的四边形为菱形?若存在,直接写出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
【答案】(1)4,3;(2)①![]() ;,②证明见解析;(3)
;,②证明见解析;(3)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)解一元二次方程求出OA,OB的长度即可;
(2)先根据三角形的面积求出点E的坐标,并根据平行四边形的对边相等的性质求出点D的坐标,然后利用待定系数法求解直线的解析式;分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;
(3)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.
(1)方程![]() ,
,
分解因式得:![]() ,
,
可得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ;
;
故答案为4,3;
(2)①根据题意,设![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴点![]() 的坐标是
的坐标是![]() ,
,
设经过![]() 、
、![]() 两点的直线的解析式为
两点的直线的解析式为![]() ,
,
则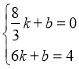 ,
,
解得: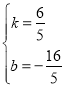 ,
,
∴解析式为![]() ;
;
②如图,
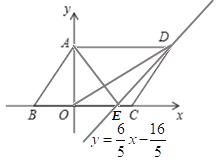
在![]() 与
与![]() 中,
中, ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)根据计算的数据,![]() ,
,
∵![]() ,
,
∴![]() 平分
平分![]() ,
,
分四种情况考虑:
①![]() 、
、![]() 是邻边,点
是邻边,点![]() 在射线
在射线![]() 上时,
上时,![]() ,
,
∴点![]() 与
与![]() 重合,即
重合,即![]() ;
;
②![]() 、
、![]() 是邻边,点
是邻边,点![]() 在射线
在射线![]() 上时,
上时,![]() 应在直线
应在直线![]() 上,且
上,且![]() 垂直平分
垂直平分![]() ,
,
此时点![]() 坐标为
坐标为![]() ;
;
③![]() 是对角线时,做
是对角线时,做![]() 垂直平分线
垂直平分线![]() ,
,![]() 解析式为
解析式为![]() ,直线
,直线![]() 过
过![]() ,且
,且![]() 值为
值为![]() (平面内互相垂直的两条直线
(平面内互相垂直的两条直线![]() 值乘积为-1),
值乘积为-1),
∴![]() 解析式为
解析式为![]() ,
,
联立直线![]() 与直线
与直线![]() ,得:
,得: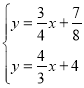 ,
,
解得:![]() ,
,![]() ,
,
∴![]() ;
;
④![]() 是对角线时,过
是对角线时,过![]() 作
作![]() 垂线,垂足为
垂线,垂足为![]() ,
,
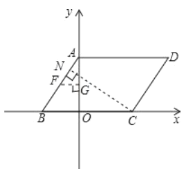
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得![]() ,即
,即![]() ,
,
做![]() 关于
关于![]() 的对称点,记为
的对称点,记为![]() ,
,![]() ,
,
过![]() 做
做![]() 轴垂线,垂足为
轴垂线,垂足为![]() ,
,![]() ,
,
∴![]() ,
,
综上所述,满足条件的点有四个:![]() ;
;![]() ;
;![]() ;
;![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某健身器材公司销售A,B两款跑步机,这两款跑步机的进价和售价如下表所示:
| A | B |
进价 | 4500 | 6200 |
售价 | 6000 | 8000 |
该公司计划购进两款跑步机若干台,共需![]() 万元,全部销售后可获利
万元,全部销售后可获利![]() 万元.
万元.
![]() 问该公司计划购进A,B两款跑步机各多少台?
问该公司计划购进A,B两款跑步机各多少台?
![]() 为了适应市场需求的变化,该公司决定在原计划的基础上,减少A款跑步机的购进数量,增加B款跑步机的购进数量,已知B款跑步机增加的数量是A款跑步机减少的数量的2倍.若用于购进这两种款跑步机的总资金不超过29.6万元,问A种款跑步机购进数量至多减少多少台?
为了适应市场需求的变化,该公司决定在原计划的基础上,减少A款跑步机的购进数量,增加B款跑步机的购进数量,已知B款跑步机增加的数量是A款跑步机减少的数量的2倍.若用于购进这两种款跑步机的总资金不超过29.6万元,问A种款跑步机购进数量至多减少多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
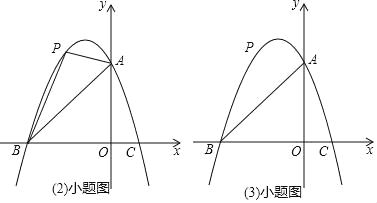
【题目】已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
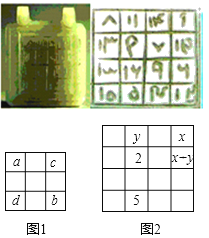
【题目】如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉﹣﹣明白玉幻方.其背面有方框四行十六格,为四阶幻方(从1到16,一共十六个数目,它们的纵列、横行与两条对角线上4个数相加之和均为34).小明探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数a,b,c,d有如图1的位置关系时,均有a+b=c+d=17.如图2,已知此幻方中的一些数,则x的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() r,则称点P为⊙O的“随心点”.
r,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(4,0),B(0,3),C(![]() ,﹣
,﹣![]() ),D(﹣
),D(﹣![]() ,﹣2)中,⊙O的“随心点”是 ;
,﹣2)中,⊙O的“随心点”是 ;
(2)若点E(6,8)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=4时,直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三点,其中t>0,函数![]() 的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com