
����Ŀ����֪����ʽ![]() �ǹ���
�ǹ���![]() �Ķ��ζ���ʽ��
�Ķ��ζ���ʽ��
��1������գ�![]() ______��
______��![]() ______��
______��![]() ______��
______��
��2����ͼ����![]() ��
��![]() �������߶�
�������߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ����ֱ����߶�
����ֱ����߶�![]() ��
��![]() ���е㣬��
���е㣬��![]() �����߶�
�����߶�![]() �ij���
�ij���
![]()
��3����ͼ����![]() ��
��![]() ��
��![]() �ֱ���������
�ֱ���������![]() ��
��![]() ��
��![]() �����ʾ������
�����ʾ������![]() ����
����![]() �㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬����������
�㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬����������![]() ��
��![]() ��������ͬʱ��ʼ�˶������е�
��������ͬʱ��ʼ�˶������е�![]() ����2����λÿ����ٶȴ�
����2����λÿ����ٶȴ�![]() ���˶���
���˶���![]() �㣬����5����λÿ����ٶ��˶���
�㣬����5����λÿ����ٶ��˶���![]() �㣬�����8����λÿ����ٶȷ��ص�
�㣬�����8����λÿ����ٶȷ��ص�![]() ��ֹͣ�˶���������
��ֹͣ�˶���������![]() ����2����λÿ����ٶȴ�
����2����λÿ����ٶȴ�![]() ���˶���
���˶���![]() �㣬����12����λÿ����ٶȷ��ص�
�㣬����12����λÿ����ٶȷ��ص�![]() ��ֹͣ�˶����ڴ��˶������У�
��ֹͣ�˶����ڴ��˶������У�![]() ��
��![]() ���㵽
���㵽![]() ��ľ����Ƿ����ȣ�����ȣ���ֱ��д����ʱ��
��ľ����Ƿ����ȣ�����ȣ���ֱ��д����ʱ��![]() �������ϱ�ʾ������������ȣ���˵�����ɣ�
�������ϱ�ʾ������������ȣ���˵�����ɣ�
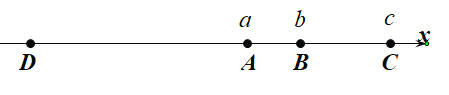
���𰸡���1��2��4��8����2��28����3������ȣ���ʱ��![]() �������ϱ�ʾ������4��
�������ϱ�ʾ������4��![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ö���ʽ�Ķ��壬�ó�x�Ĵ�����ϵ�������ó��𰸣�
��2������![]() �Լ���1���Ľ�����EG��GH��HF�ij��������߶εĺͲ��ʾ��MN����MN=10���ɵó��𰸣�
�Լ���1���Ľ�����EG��GH��HF�ij��������߶εĺͲ��ʾ��MN����MN=10���ɵó��𰸣�
��3����t���![]() ��
��![]() ���㵽
���㵽![]() ��ľ�����ȣ��ֱ���t��ʾ��AQ��AP���������̽�����⣮
��ľ�����ȣ��ֱ���t��ʾ��AQ��AP���������̽�����⣮
�⣺��1���߶���ʽ![]() �ǹ���
�ǹ���![]() �Ķ��ζ���ʽ��
�Ķ��ζ���ʽ��
��a-2=0��![]() =2��b+4��0��c-8=0��
=2��b+4��0��c-8=0��
��a=2��b=4��c=8��
��2����![]() ��a=2��b=4��c=8��
��a=2��b=4��c=8��

��EG=2x��GH=4x��HF=8x��
��EF=14x��EH=6x��GF=12x��
��![]() ��
��![]() ����ֱ����߶�
����ֱ����߶�![]() ��
��![]() ���е㣬
���е㣬
��MH=3x��NF=6x��HN=HF-NF=2x��
��MN=MH+HN=5x=10��
��x=2��
��EF=14x=14��2=28��
��3����t���![]() ��
��![]() ���㵽
���㵽![]() ��ľ�����ȣ�
��ľ�����ȣ�

��![]() ��
��![]() ��
��![]() �ֱ���������
�ֱ���������![]() ��
��![]() ��
��![]() �����ʾ������
�����ʾ������![]() ����
����![]() �㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬a=2��b=4��c=8��
�㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬a=2��b=4��c=8��
��D���ʾ������-8��
��AD=10��AB=2��BC=4��AC=6��
��0<t��3ʱ����ͼ1��
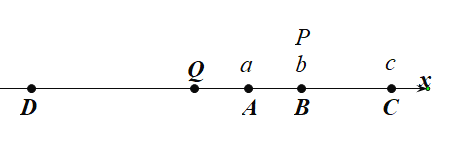
������ã� PC=BQ=2t��AP=AQ��
��AC-PC=BQ-AB��
��6-2t=2t-2��
��ã�t=2��
���![]() �������ϱ�ʾ������8-PC=8-2t=4��
�������ϱ�ʾ������8-PC=8-2t=4��
��3<t��5ʱ����ͼ2��
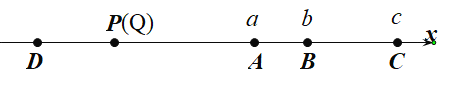
������ã�AP=AQ��BQ=2t��AP=5(t-3)��
��AP=BQ-AB����5(t-3)= 2t-2��
��ã�t=![]() ��
��
��AP=2t-2=![]() ��
��
���![]() �������ϱ�ʾ������
�������ϱ�ʾ������![]() =
=![]() ��
��
��5<t��6ʱ����ͼ3��

������ã�AP=AQ��BQ=2t��DP= 8(t-5)��DQ=12-2t��
��8(t-5)= 12-2 t��
��ã�t=![]() ��
��
��BQ =2t=![]() ��
��
���![]() �������ϱ�ʾ������
�������ϱ�ʾ������![]() =
=![]() ��
��
��6<t��5ʱ����ͼ4��
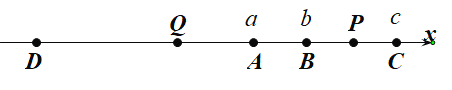
������ã�AP=AQ��AQ=10-12(t-6)��DP=8(t-5)��
��AP=DP-AD����10-12(t-6)= 8(t-5)-10��
��ã�t=![]() ��
��
��AP= 8(t-5)-10=![]() ��
��
���![]() �������ϱ�ʾ������
�������ϱ�ʾ������![]() =
=![]() ��
��
��![]() ��
��![]() ���㵽
���㵽![]() ��ľ������ʱ��
��ľ������ʱ��![]() �������ϱ�ʾ������4��
�������ϱ�ʾ������4��![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ���ɣ�1��~��2���⣺
��ѧ���ϣ���ʦ��ʾ��һ���⣺��ͼ1����һ��ֱ�����ǰ�![]() ��ֱ�DZ�
��ֱ�DZ�![]() �ڷ���ֱ��
�ڷ���ֱ��![]() �ϣ�Ȼ����ֱ�Ƕ���
�ϣ�Ȼ����ֱ�Ƕ���![]() Ϊ��ת����˳ʱ����ת������ǰ壮������
Ϊ��ת����˳ʱ����ת������ǰ壮������![]() ƽ��
ƽ��![]() ��̽��
��̽��![]() ��
��![]() ��������ϵ����˵������һ��ʱ���˼����ͬѧ�ǿ�ʼ�˽�����
��������ϵ����˵������һ��ʱ���˼����ͬѧ�ǿ�ʼ�˽�����
С�����Ҹ�����ʦ����������ͼ2�����������![]() ʱ��
ʱ��![]() �Ķ�����
�Ķ�����![]() ��
��
С�죺��С����ͼ���У���![]() ��
��![]() ����
����![]() ���Ϸ����ҷ��֣�����������£�
���Ϸ����ҷ��֣�����������£�![]() ʼ����
ʼ����![]() ���ڲ�������
���ڲ�������![]() �Ķ�����
�Ķ�����![]() ��ͨ�����㣬
��ͨ�����㣬![]() �Ķ��������ú�
�Ķ��������ú�![]() ��ʽ�ӱ�ʾ���õ�
��ʽ�ӱ�ʾ���õ�![]() ��
��![]() ��������ϵ��
��������ϵ��![]() ��
��
С�����ҳ��˻�С��������ͼ�Σ����������༸�֣�Ҳ�ֱ�ó�![]() ��
��![]() ��������ϵ���Ӷ��������ʦ��������⣮
��������ϵ���Ӷ��������ʦ��������⣮
��ʦ����Щͬѧ���Ȼ���ͼ�Σ��ٽ�����⣬��������ͼ�ε�ֱ�ԣ���Ҫע��һ�㣬�ڳ��н������о��ĽǶ���С��![]() �ģ����Ŵ�ҽ��������룬��
�ģ����Ŵ�ҽ��������룬��![]() ��λ����
��λ����![]() �Ϸ���ֱ��
�Ϸ���ֱ��![]() �⣬
�⣬![]() ��ֵ�����ֵ���ĸ���������˴����һ���˼�룬ͬѧ���ٸ���С����˵�Ľ���̽�������ܹ��ɳ���������ѧ˼�뷽����
��ֵ�����ֵ���ĸ���������˴����һ���˼�룬ͬѧ���ٸ���С����˵�Ľ���̽�������ܹ��ɳ���������ѧ˼�뷽����
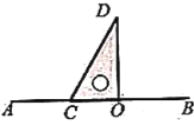
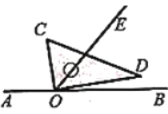
ͼ1 ͼ2
��1����ͼ2����![]() ��
��![]() ����
����![]() �Ϸ���
�Ϸ���![]() ��
��
���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() Ϊ_____________��
Ϊ_____________��
��С��ġ�![]() ʼ����
ʼ����![]() ���ڲ�����˵������ȷ����Ϊʲô��
���ڲ�����˵������ȷ����Ϊʲô��
��2�����������������![]() ��
��![]() ��������ϵ��˵����
��������ϵ��˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����![]() ��,
��,![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����
�����![]() ��
��![]() ���ٶ��ƶ���ͬʱ��
���ٶ��ƶ���ͬʱ��![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����
�����![]() ��
��![]() ���ٶ��ƶ�����һ���㵽���յ�ʱ��һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ
���ٶ��ƶ�����һ���㵽���յ�ʱ��һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ![]() �룬
�룬

![]() �� ���
�� ��� ![]() ���������
���������![]()
![]() �� ���
�� ���![]() �ij��ȵ���
�ij��ȵ���![]()
![]() �˶������У��ı���APQC������ܷ����
�˶������У��ı���APQC������ܷ����![]() ��˵�����ɣ�
��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij��˾�����βɹ���һ�����⣬��һ�λ���40��Ԫ���ڶ��λ���60��Ԫ����֪��һ�βɹ�ʱÿ�ִ���ļ۸��ȥ���ƽ���۸�������500Ԫ���ڶ��βɹ�ʱÿ�ִ���ļ۸��ȥ���ƽ���۸��½���500Ԫ���ڶ��βɹ��������ǵ�һ�βɹ�����������.
��1������ȥ��ÿ�ִ����ƽ���۸��Ƕ���Ԫ��
��2���ù�˾�ɽ�����ӹ�����ۻ���Ƭ���������ӹ�����ۣ�ÿ��ɼӹ�8�ִ��⣬ÿ�ִ������1000Ԫ���������ӹ�����Ƭ��ÿ��ɼӹ�12�ִ��⣬ÿ�ִ������600Ԫ.Ϊ������Ҫ�����вɹ��Ĵ��������30���ڼӹ���ϣ��Ҽӹ���۵Ĵ������������ڼӹ���Ƭ�Ĵ���������һ��.Ϊ����������Ӧ�����ٶִ���ӹ�����ۣ��������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺С���Ȱ���ѧ���ڿ������Ͽ�����һ����Ȥ�Ķ������������߳������������������ߵ�ƽ���͵��ڵ����ߵ�һ����������ϵ����ߵ�ƽ���͵���������ͼ1���ڡ�ABC�У���DΪBC���е㣬���ݡ����߳����������ɵã�
AB2��AC2��2AD2��2BD2��
С�����Զ�������֤�������ֹ������£�
�⣺����A��AE��BC�ڵ�E����ͼ2����Rt��ABE�У�AB2��AE2��BE2��
ͬ���ɵã�AC2��AE2��CE2��AD2��AE2��DE2��
Ϊ֤���ķ��㣬������BD��CD��x��DE��y��
��AB2��AC2��AE2��BE2��AE2��CE2������
��1���������С��ʣ���֤�����̣�
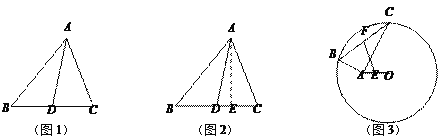
�������ã�
��2�� �� �ڡ�ABC�У���DΪBC���е㣬AB��6��AC��4��BC��8����AD��_______��
�� ��ͼ3����O�İ뾶Ϊ6����A��Բ�ڣ���OA��2![]() ����B�͵�C�ڡ�O�ϣ��ҡ�BAC��90�㣬��E��F�ֱ�ΪAO��BC���е㣬��EF�ij�Ϊ________��
����B�͵�C�ڡ�O�ϣ��ҡ�BAC��90�㣬��E��F�ֱ�ΪAO��BC���е㣬��EF�ij�Ϊ________��
��չ���죺
��3��С�����������������뵽������ѵ�����ϵ���Ŀ����ͼ4����֪��O�İ뾶Ϊ5![]() ����A(3��4)Ϊֱ�Ƕ���ġ�ABC������������B��C���ڡ�O�ϣ�DΪBC���е㣬��AD�������ֵ��������������ķ����ͽ��ۣ����AD�������ֵ��
����A(3��4)Ϊֱ�Ƕ���ġ�ABC������������B��C���ڡ�O�ϣ�DΪBC���е㣬��AD�������ֵ��������������ķ����ͽ��ۣ����AD�������ֵ��
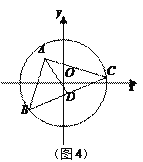
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���ABC���������㶼�ڸ���ϣ���A��B��C������ֱ�ΪA(-2��4)��B(-2��0)��C(-4��1)�����������ƽ��ֱ������ϵ����������⣺
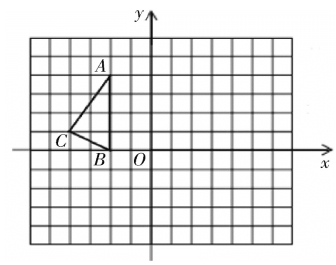
��1��������ABC����ԭ��O���ĶԳ�ͼ����A1B1C1.
��2��ƽ����ABC��ʹ��A�ƶ�����A2(0��2)������ƽ�ƺ����A2B2C2��д����B2��C2������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��B��������λ�ڵ�A���һ�㣬��AB��20������P�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�룮
![]()
��1�������ϵ�B��ʾ�������� ����P��ʾ�������� �����ú�t�Ĵ���ʽ��ʾ��
��2������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʶ�����ʱ��P��Q֮��ľ���ǡ�õ���2��
��3������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ������ֱ��д��������ʱ��P��Q֮��ľ���ǡ�õ���2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADΪ�ȱߡ�ABC�ĸߣ�E��F�ֱ�Ϊ�߶�AD��AC�ϵĶ��㣬��AE��CF����BF+CEȡ����Сֵʱ����AFB����������
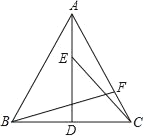
A. 112.5��B. 105��C. 90��D. 82.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ͼ4�У�����ABCD�ı߳�Ϊ3����A=60������M��AD����һ�㣬��DM=![]() AD����N������AB��BC�ϵ�һ�����㣮
AD����N������AB��BC�ϵ�һ�����㣮
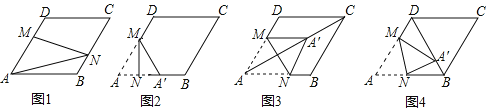
��1����ͼ1����N��BC���ϣ���MN���Խ���AC��BD�Ľ���ʱ�����߶�AN�ij���Ϊ ��
��2������N��AB����ʱ������AMN��MN���۵õ���A��MN����ͼ2��
������A������AB���ϣ����߶�AN�ij���Ϊ ��
�ڵ���A�����ڶԽ���AC��ʱ����ͼ3����֤���ı���AM A��N�����Σ�
�۵���A�����ڶԽ���BD��ʱ����ͼ4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com