
| 线段PQ的长度 | 线段PB的长度 | |
| 第一次 | ||
| 第二次 |
3
| ||
| 8 |
| 1 |
| 16 |
| 1 |
| 2 |
3
| ||
| 8 |
3
| ||
| 8 |
| 1 |
| 16 |
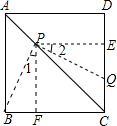 解:(1)(说明:表略,两线段长度基本相等即可)经测量,得PB=PQ
解:(1)(说明:表略,两线段长度基本相等即可)经测量,得PB=PQ| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 16 |
3
| ||
| 4 |
3
| ||
| 4 |
3
| ||
| 4 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 16 |
3
| ||
| 4 |
3
| ||
| 8 |
| 1 |
| 16 |
3
| ||
| 4 |
3
| ||
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
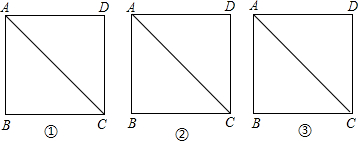
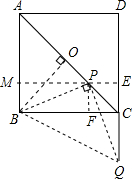
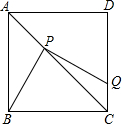 如图,将一把三角尺放在边长为1的正方形ABCD上使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论.
如图,将一把三角尺放在边长为1的正方形ABCD上使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com