
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | a | 0.64 | 0.58 | b | 0.60 | 0.601 |
分析 (1)利用频率=频数÷样本容量直接求解即可;
(2)根据统计数据,当n很大时,摸到白球的频率接近0.60;
(3)根据利用频率估计概率,可估计摸到白球的概率为0.60,然后利用概率公式计算白球的个数.
解答 解:(1)a=$\frac{59}{100}$=0.59,b=$\frac{290}{500}$=0.58,
故答案为:0.59,0.58;
(2)“摸到白球”的概率的估计值是0.60,
故答案为:0.60;
(3)由(2)摸到白球的概率为0.60,
所以可估计口袋中白种颜色的球的个数=20×0.6=12(个),黑球20-12=8(个).
答:黑球8个,白球12个.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:判断题
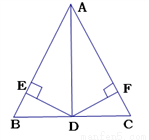
如图,在△ABC中.AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若AD=2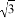 ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
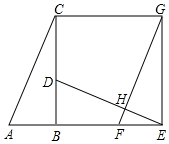 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
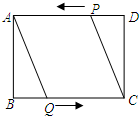 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,同时点Q从点B向点C运动,点P,Q的速度都是1cm/s.
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,同时点Q从点B向点C运动,点P,Q的速度都是1cm/s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com