
 вбжЊЃКШчЭМЃЌЖдГЦжсЮЊжБЯп$x=\frac{3}{2}$ЕФХзЮяЯпy=ax2+bx+cгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгBCЁЂACЃЌЧвOB=$\frac{1}{2}$OA=$\frac{1}{3}$OCЃЎ
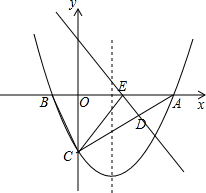
вбжЊЃКШчЭМЃЌЖдГЦжсЮЊжБЯп$x=\frac{3}{2}$ЕФХзЮяЯпy=ax2+bx+cгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгBCЁЂACЃЌЧвOB=$\frac{1}{2}$OA=$\frac{1}{3}$OCЃЎЗжЮі ЃЈ1ЃЉИљОнAЁЂBЙигкx=$\frac{3}{2}$ЖдГЦЃЌМАOB=$\frac{1}{2}$OA=$\frac{1}{3}$OCЃЌПЩЕУAЁЂBЁЂCЕФзјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУACЁЂBCЕФНтЮіЪНЃЌИљОнPдкACЩЯЃЌПЩЕУPЕузјБъЃЌИљОнPMЁЭxжсгкЕуMЃЌПЩЕУPMЕФГЄЃЌИљОнPQЁЮxжсНЛBCгкЕуQЃЌПЩЕУQЕуЕФзјБъЃЌИљОне§ЗНаЮЕФБпГЄЯрЕШЃЌПЩЕУЙигкaЕФЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУPЕузјБъЃЛ
ЃЈ3ЃЉИљОнЦНааЯпМфЕФЙиЯЕЃЌПЩЕУDEЕФНтЮіЪНЃЌИљОнСЊСЂЗНГЬзщЃЌПЩЕУDЕузјБъЃЌИљОнЙДЙЩЖЈРэЃЌПЩЕУEDЕФГЄЃЌИљОнЦНааЯпМфЕФОрРыЯрЕШЃЌПЩЕУEЕНBCЕФОрРыгыCЕНDEЕФОрРыЯрЕШЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌПЩЕУЖўДЮКЏЪ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЃЌПЩЕУmЕФжЕЃЌИљОнДњЪ§ЪНЧѓжЕЃЌПЩЕУД№АИЃЎ
НтД№ НтЃКЃЈ1ЃЉгЩХзЮяЯпy=ax2+bx+cгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгBCЁЂACЃЌЧвOB=$\frac{1}{2}$OA=$\frac{1}{3}$OCЃЌ
ЩшOB=-aЃЌOA=2aЃЌOC=-3aЃЎ
гЩABЙигкx=$\frac{3}{2}$ЖдГЦЃЌЕУ
$\frac{-a+2a}{2}$=$\frac{3}{2}$ЃЌ
НтЕУa=3ЃЌBЃЈ3ЃЌ0ЃЉЃЌAЃЈ6ЃЌ0ЃЉЃЌCЃЈ0ЃЌ-9ЃЉЃЎ
НЋAЁЂBЁЂCЕуЕФзјБъДњШыХзЮяЯпНтЮіЪНЃЌЕУ
$\left\{\begin{array}{l}{9a-3b+c=0}\\{36a+6b+c=0}\\{c=-9}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=-9}\end{array}\right.$ЃЌ
ХзЮяЯпЕФКЏЪ§БэДяЪНy=$\frac{1}{2}$x2-$\frac{3}{2}$x-9ЃЛ
ЃЈ2ЃЉЩшACЕФНтЮіЪНЮЊy=k1x+b1ЃЌ
НЋAЁЂCЕузјБъЃЌЕУ$\left\{\begin{array}{l}{-6{k}_{1}+{b}_{1}=0}\\{{b}_{1}=-9}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{{k}_{1}=\frac{3}{2}}\\{{b}_{1}=9}\end{array}\right.$ЃЌ
ACЕФНтЮіЪНЮЊy=$\frac{3}{2}$x-9ЃЌ
PдкACЩЯЃЌЩшPЕузјБъЮЊЃЈaЃЌ$\frac{3}{2}$a-9ЃЉЃЌPM=|$\frac{3}{2}$a-9|ЃЎ
BCЕФНтЮіЪНЮЊy=-3x-9ЃЌ
PQЁЮxжсQЕуЕФзнзјБъЮЊ$\frac{3}{2}$a-9ЃЌ
НЋQЕуЕФзнзјБъДњШыКЏЪ§НтЮіЪНЃЌЕУ-3x-9=$\frac{3}{2}$a-9ЃЌ
НтЕУx=-$\frac{a}{2}$ЃЎ
PQ=a-ЃЈ-$\frac{a}{2}$ЃЉ=$\frac{3}{2}$aЃЌ
гЩЫФБпаЮPMNQЮЊе§ЗНаЮЃЌЕУPQ=PMЃЌМД$\frac{3}{2}$a=$\frac{3}{2}$a-9Лђ$\frac{3}{2}$a=9-$\frac{3}{2}$aЃЌ
НтЕУa=3ЃЌ$\frac{3}{2}$a-9=-$\frac{9}{2}$ЃЌ
ЫФБпаЮPMNQЮЊе§ЗНаЮЪБЕуPЕФзјБъЪЧЃЈ3ЃЌ-$\frac{9}{2}$ЃЉЃЛ
ЃЈ3ЃЉEЕузјБъЮЊЃЈ6-mЃЌ0ЃЉЃЌЕуEзїжБЯпlЦНааBCЃЌ
ЩшDEЕФНтЮіЪНЮЊy=-3x+bЃЌНЋEЕузјБъДњШыЃЌЕУ
-3ЃЈ6-mЃЉ+b=0ЃЌЃЎНтЕУb=18-3mЃЌ
DEЕФНтЮіЪНЮЊy=-3x+18-3mЃЌ
СЊСЂDEгыACЃЌЕУ
$\left\{\begin{array}{l}{y=-3x+18-3m}\\{y=\frac{3}{2}x-9}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{x=6-\frac{2}{3}m}\\{y=-m}\end{array}\right.$ЃЌ
DЕузјБъЮЊЃЈ6-$\frac{2}{3}$mЃЌ-mЃЉЃЌ
гЩЙДЙЩЖЈРэЃЌЕУDE=$\sqrt{[ЃЈ6-mЃЉ-ЃЈ6-\frac{2}{3}mЃЉ]^{2}+{m}^{2}}$=$\frac{\sqrt{10}}{3}$mЃЌ
EЕНBCЕФОрРы$\frac{|3ЃЈ6-mЃЉ+0+9|}{\sqrt{ЃЈ-3ЃЉ^{2}+1}}$=$\frac{|27-3m|}{\sqrt{10}}$ЃЌ
EЕНBCЕФОрРыгыDЕНBCЕФОрРыЯрЕШЃЌЕУDЕНBCЕФОрРыЪЧ$\frac{27-3m}{\sqrt{10}}$ЃЌ
SЁїCDE=$\frac{1}{2}$•$\frac{27-3m}{\sqrt{10}}$$•\frac{\sqrt{10}m}{3}$=$\frac{1}{2}$[ЃЈ-ЃЈm-$\frac{9}{2}$ЃЉ2+$\frac{81}{4}$]
ЕБm=$\frac{9}{2}$ЪБЃЌSЁїCDEзюДѓЃЎ
МДm=$\frac{9}{2}$ЃЌSЁїCDEзюДѓЪБЃЌDЕНBCЕФОрРыЪЧ$\frac{27-3m}{\sqrt{10}}$=$\frac{27-3ЁС\frac{9}{2}}{\sqrt{10}}$=$\frac{27\sqrt{10}}{20}$ЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§злКЯЬтЃЌЃЈ1ЃЉРћгУAЁЂBЙигкx=$\frac{3}{2}$ЖдГЦЃЌМАOB=$\frac{1}{2}$OA=$\frac{1}{3}$OCЕУГіAЁЂBЁЂCЕФзјБъЪЧНтЬтЙиМќЃЛЃЈ2ЃЉРћгУЭМЯѓЩЯЕФЕуТњзуКЏЪ§НтЮіЪНЕУГіPЕузјБъЃЌгжРћгУЦНаагкxжсЕФжБЯпЩЯЕуЕФзнзјБъЯрЕШЕУГіQЕузјБъЃЌРћгУе§ЗНаЮЕФаджЪЕУГіЙигкaЕФЗНГЬЪЧНтЬтЙиМќЃЛЃЈ3ЃЉРћгУРћгУНтЗНГЬзщЕУГіDЕузјБъЃЌРћгУЙДЙЩЖЈРэЕУГіDEЕФГЄЃЌРћгУЦНааЯпМфЕФОрРыЯрЕШЕУГіEЕНBCЕФОрРыгыCЕНDEЕФОрРыЯрЕШЪЧНтЬтЙиМќЃЌгжРћгУСЫЖўДЮКЏЪ§ЕФаджЪЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\left\{\begin{array}{l}{x-3=0}\\{3x-2y=7}\end{array}\right.$ | BЃЎ | $\left\{\begin{array}{l}{2x-y=3}\\{3xy=8}\end{array}\right.$ | ||
| CЃЎ | $\left\{\begin{array}{l}{x+y=3}\\{x-z=5}\end{array}\right.$ | DЃЎ | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{3}{y}=4}\\{\frac{1}{3}x+\frac{1}{2}y=1}\end{array}\right.$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЁЯBAD=60ЁуЃЌAB=6ЃЌAC=6$\sqrt{3}$ЃЌЧѓ?ABCDЕФУцЛ§ЃЎ
ШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЁЯBAD=60ЁуЃЌAB=6ЃЌAC=6$\sqrt{3}$ЃЌЧѓ?ABCDЕФУцЛ§ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌгаГЄЮЊ24cmЕФРщАЪЃЌвЛУцРћгУЧНЃЈЧНГЄ10mЃЉЮЇГЩжаМфИєЕРРщАЪЕФГЄЗНаЮЛЈЦдЃЌЩшЛЈЦдЕФПэABЮЊxЃЈmЃЉЃЌУцЛ§ЮЊyЃЈm2ЃЉЃЎ
ШчЭМЃЌгаГЄЮЊ24cmЕФРщАЪЃЌвЛУцРћгУЧНЃЈЧНГЄ10mЃЉЮЇГЩжаМфИєЕРРщАЪЕФГЄЗНаЮЛЈЦдЃЌЩшЛЈЦдЕФПэABЮЊxЃЈmЃЉЃЌУцЛ§ЮЊyЃЈm2ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌCBЁЭABЃЌDAЁЭABЃЌДЙзуЗжБ№ЪЧAЁЂBЃЌAB=BCЃЌEЪЧABжаЕуЃЌCEЁЭDBЃЌCEНЛBDгкЕуOЃЎЯТСаНсТлЃКЂйBE=ADЃЛЂкACДЙжБЦНЗжDEЃЛЂлЁЯDBC=ЁЯDCBЃЛЂмЁЯCED=ЁЯDBCЃЛЂнBC=CDЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
ШчЭМЃЌCBЁЭABЃЌDAЁЭABЃЌДЙзуЗжБ№ЪЧAЁЂBЃЌAB=BCЃЌEЪЧABжаЕуЃЌCEЁЭDBЃЌCEНЛBDгкЕуOЃЎЯТСаНсТлЃКЂйBE=ADЃЛЂкACДЙжБЦНЗжDEЃЛЂлЁЯDBC=ЁЯDCBЃЛЂмЁЯCED=ЁЯDBCЃЛЂнBC=CDЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ| AЃЎ | ЂйЂкЂл | BЃЎ | ЂйЂлЂн | CЃЎ | ЂйЂкЂм | DЃЎ | ЂкЂлЂн |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com