
分析 先算除法,再算减法,最后把a的值代入进行计算即可.
解答 解:原式=$\frac{4}{a+3}$-$\frac{6}{(a+3)(a-3)}$•$\frac{a-3}{2}$
=$\frac{4}{a+3}$-$\frac{3}{a+3}$
=$\frac{1}{a+3}$,
当a=$\sqrt{3}$时,原式=$\frac{1}{3+\sqrt{3}}$=1-$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,(1)求∠AFD的度数;(2)当BC=4cm时,求△ACE的面积.
如图,在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,(1)求∠AFD的度数;(2)当BC=4cm时,求△ACE的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
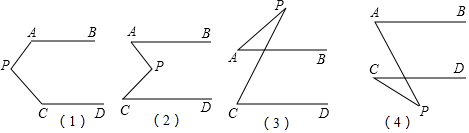
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )
如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )| A. | 2 | B. | 1 | C. | 0.5 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
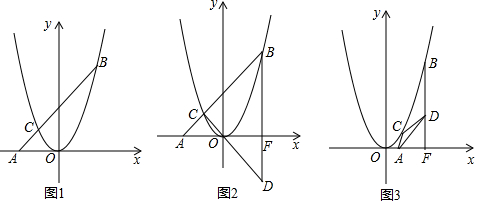
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com