
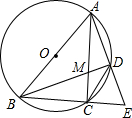
 如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.
如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.分析 (1)要证明BC•CE=AC•MC,即证明$\frac{BC}{AC}$=$\frac{MC}{CE}$,即证明△CBM∽△CAE;
(2)因为点D是劣弧$\widehat{AC}$的中点,所以$\widehat{AD}$=$\widehat{CD}$,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MD•BD=10,再由tan∠ACD=tan∠ABD=$\frac{1}{3}$求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
(3)因为CD∥AB,AF∥BC,所以△CDE∽△BAE,△ADF∽△DEC,利用对边的比相等可得$\frac{BC}{CE}$=$\frac{DF}{CD}$,所以$\frac{CF}{CD}$-$\frac{BC}{CE}$=$\frac{CF}{CD}$-$\frac{DF}{CD}$.
解答 解:(1)∵$\widehat{CD}$=$\widehat{CD}$,
∴∠MBC=∠CAE,
∵AB是⊙O的直径,
∴∠BCM=∠ACE=90°,
∴△CBM∽△CAE,
∴$\frac{BC}{AC}$=$\frac{MC}{CE}$,
∴BC•CE=AC•MC;
(2)∵点D是劣弧$\widehat{AC}$的中点,
∴$\widehat{AD}$=$\widehat{CD}$;
∴∠ABD=∠MBC,∠ACD=∠CAE
∵∠MBC=∠CAE,
∴∠ABD=∠CAE=∠ACD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴△AMD∽△BAD,
∴$\frac{MD}{AD}$=$\frac{AD}{BD}$,
∴AD2=MD•BD=10,
∴AD=$\sqrt{10}$,
∵tan∠ACD=tan∠ABD=$\frac{1}{3}$
∴$\frac{AD}{BD}=\frac{1}{3}$,
∴BD=3$\sqrt{10}$
∵AB2=AD2+BD2,
∴AB=$\sqrt{(\sqrt{10})^{2}+(3\sqrt{10})^{2}}$=10
∴⊙O的半径为:$\frac{1}{2}$AB=5;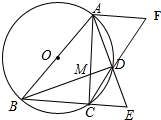 (3)∵CD∥AB,
(3)∵CD∥AB,
∴△CDE∽△BAE,
∴$\frac{BC}{CE}$=$\frac{AD}{DE}$,
∵AF∥CE,
∴△ADF∽△DEC,
∴$\frac{AD}{DE}$=$\frac{DF}{CD}$,
∴$\frac{BC}{CE}$=$\frac{DF}{CD}$,
∴$\frac{CF}{CD}$-$\frac{BC}{CE}$=$\frac{CF}{CD}$-$\frac{DF}{CD}$=$\frac{CF-DF}{CD}$=$\frac{CD}{CD}=1$.
点评 此题属于圆的综合题,涉及了相似三角形的判定与性质、三角函数值的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
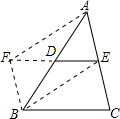 完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com