
 如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D,(推理时不需要写出每一步的理由)
如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D,(推理时不需要写出每一步的理由)分析 (1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN=60°+∠DBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
解答 解:
(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角相等?两直线平行,④a∥b,b∥c⇒a∥c.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
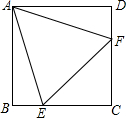 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 值日老师调查各班学生的出勤情况 | |
| B. | 调查凉山州中学生参加体育锻炼的时间 | |
| C. | 了解某班女学生的身高情况 | |
| D. | 了解全班同学的课外读书时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 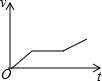 | B. | 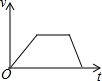 | C. | 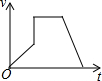 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com