
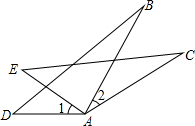
 已知:∠D=∠E,AD=AE,∠1=∠2.求证:BD=CE.
已知:∠D=∠E,AD=AE,∠1=∠2.求证:BD=CE.  百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{{\sqrt{2}}}$ | B. | $2\sqrt{a}$ | C. | 4$\sqrt{a}$ | D. | $\frac{{2\sqrt{a}}}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{3}{2}}÷\sqrt{\frac{1}{18}}=3\sqrt{3}$ | B. | $(\sqrt{8}+\sqrt{3})×\sqrt{6}=4\sqrt{3}+3\sqrt{2}$ | C. | $(4\sqrt{2}-3\sqrt{6})÷2\sqrt{2}=4-3\sqrt{3}$ | D. | $(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})=2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
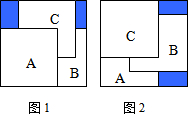 把三张大小相同的正方形卡片A,B,C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图1、图2摆放,阴影部分的面积分别为S1和S2,则S1和S2的大小关系是( )
把三张大小相同的正方形卡片A,B,C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图1、图2摆放,阴影部分的面积分别为S1和S2,则S1和S2的大小关系是( )| A. | S1=S2 | B. | S1<S2 | C. | S1>S2 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com