
����Ŀ������������10�֣���M�ص�N����һ����ͨ��·����·��Ϊ120km����һ�����ٹ�·����·��Ϊ126km���׳����ҳ�ͬʱ��M�ؿ���N�أ��׳�ȫ������ͨ��·���ҳ�����ʻ����һ����ͨ��·��Ȼ�����ϸ��ٹ�·��������������ͨ��·���ٹ�·�Ϸֱ𱣳�������ʻ����������ͨ��·�ϵ��г��ٶ�Ϊ60km/h���ڸ��ٹ�·�ϵ��г��ٶ�Ϊ100km/h������������x hʱ����N�ص�·��Ϊy km��ͼ�е��߶�AB������ACD�ֱ��ʾ�׳����ҳ���y��x֮��ĺ�����ϵ��
��1����գ�a�� ��b�� ��
��2�����߶�AB��CD����ʾ��y��x֮��ĺ�����ϵʽ��
��3�������ں�ʱ�������N�ص�·��֮��ﵽ��30km��

���𰸡���1��1.36��2����2��y1=��60x+120��y2=��100x+136��
��3����1.15��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��
�������������������1�����C���꣬�ٸ���ʱ��=·�����ٶȷֱ�����׳�����ͨ��·����ʻ��ʱ�估�ҳ��ڸ��ٹ�·����ʻ��ʱ�䣬�ɵ�a��b��ֵ��
��2������A��B��C��D�ĵ��������ϵ�������ɵ��߶�AB��CD����ʾ��y��x֮��ĺ�����ϵʽ��
��3���������ۣ���0��x��0.1ʱ���ɽ���ʽ��֪�ס���������������Ϊ12����0.1��x��1.36ʱ����y1��y2��30�в���ʽ�ɵ�x�ķ�Χ����1.36��x��2ʱ����y1��30�в���ʽ�ɵô�ʱx�ķ�Χ���ۺ�������������ɵô𰸣�
�����������1���������⣬֪����C������Ϊ��0.1��126����
��a=0.1+![]() =1.36��b=
=1.36��b=![]() =2��
=2��
�ʴ�Ϊ��1.36��2��
��2�����߶�AB����ʾ��y��x֮��ĺ�����ϵʽ�ֱ�Ϊy1=k1x+b1��
��A��0��120����B��2��0�����������ã�
![]() ��
��
��ã� ![]() ��
��
��y1=��60x+120��
���߶�CD����ʾ��y��x֮��ĺ�����ϵʽ�ֱ�Ϊy2=k2x+b2��
��C��0.1��126����D��1.36��0�����������ã�
![]() ��
��
��ã� ![]() ��
��
��y2=��100x+136��
��3�������⣬����x=0.1ʱ��������N�ص�·��֮����12km��
����0��x��0.1ʱ��������N�ص�·��֮����ܴﵽ��30km��
����0.1��x��1.36ʱ����y1��y2��30���ã���60x+120��������100x+136����30��
���x��1.15��
����1.15��x��1.36ʱ��������N�ص�·��֮��ﵽ��30km��
����1.36��x��2ʱ����y1��30������60x+120��30�����x��1.5��
����1.36��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��
���ϣ���1.15��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]()
![]() ��
��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() �����
�����![]() ���ڽ�
���ڽ�![]() �����
�����![]() �����½��ۣ���
�����½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ����У� ��
��������ȷ�Ľ����У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����õ�ʽ������1������ʽ3x��10��2x���б��Σ���ȷ����( )
A. 2x��10
B. x��10
C. ��10��x
D. 3x��2x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η��̣�a+1��x2+x+a2��1��0��һ������0����a��ֵΪ��������
A. 1 B. ��1 C. ��1 D. 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2��2x+4��Ϊy=a(x��h)2+k����ʽ��������ȷ������ ��
A. y=(x��1)2+2 B. y=(x��1)2+3
C. y=(x��2)2+2 D. y=(x��2)2+4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���У���
�Ų����ھ���ֵ��С���������Ʋ����ھ���ֵ��С��ʵ��
�Dz������뱾��������ƽ������ȵ����ȱ���ʵ��С�������Ǹ�ʵ��
�ɷǸ�ʵ������С������0
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A�������ϱ�ʾ��30�ĵ㣬B�������ϱ�ʾ10�ĵ㣬C�������ϱ�ʾ18�ĵ㣬��A��B��C��������ͬʱ��������������˶�����A�˶����ٶ���6����λ����ÿ�룬��B��C�˶����ٶ���3����λ����ÿ�룮���������˶���ʱ��Ϊt��(t��5)�����߶�OA���е�ΪP���߶�OB���е�ΪM���߶�OC���е�ΪN����2PM��PN��2ʱ��t��ֵΪ_____��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��CB������ΪC�㣬AC��CB��8cm����Q��AC���е㣬����P��B�������������BC���������ƶ�����P���˶��ٶ�Ϊ2cm/s���趯��P�˶���ʱ��Ϊts��Ϊ����˵�������Ƿֱ��������ABC���ΪS��������PCQ�����ΪS1��������PAQ�����ΪS2��������ABP�����ΪS3��
��1��S3���� ��cm2���ú�t�Ĵ���ʽ��ʾ����
��2������P�˶����룬S1��![]() S��˵�����ɣ�
S��˵�����ɣ�
��3������̽���Ƿ����ijһʱ�̣�ʹ��S1��S2��S3�������ڣ����tֵ���������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���P������Ϊ��![]() ��
��![]() ������Q��������
������Q��������![]() ��
��![]() ������
������![]() ��
��![]() ����P��QΪij�����ε��������㣬�Ҹþ��εı߾���ij�������ᴹֱ����Ƹþ���Ϊ��P��Q������ؾ���������ͼΪ��P��Q ������ؾ�������ʾ��ͼ��
����P��QΪij�����ε��������㣬�Ҹþ��εı߾���ij�������ᴹֱ����Ƹþ���Ϊ��P��Q������ؾ���������ͼΪ��P��Q ������ؾ�������ʾ��ͼ��
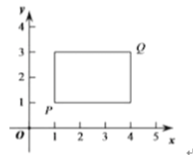
��1����֪��A������Ϊ��1��0����
������B������Ϊ��3��1�����A��B������ؾ������������
����C��ֱ��x=3�ϣ�����A��C������ؾ�����Ϊ�����Σ���ֱ��AC�ı���ʽ��
��2����O�İ뾶Ϊ![]() ����M������Ϊ��m��3����������O�ϴ���һ��N��ʹ�õ�M��N������ؾ�����Ϊ�����Σ���m��ȡֵ��Χ��
����M������Ϊ��m��3����������O�ϴ���һ��N��ʹ�õ�M��N������ؾ�����Ϊ�����Σ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com