

分析 (1)先求出抛物线对称轴,确定出点E坐标,从而求出点A,B坐标,用待定系数法求出抛物线解析式;
(2)先用锐角三角函数得出$\frac{CH}{PH}=\frac{PF}{AF}$,设出点P坐标,建立方程求出点P的坐标,即可;
(3)先判断出∠PQG=∠DMN,从而得出PQ∥x轴,求出点Q坐标,进而求出DL,ML,即可.
解答 解:(1)∵抛物线的解析式为y=ax2-ax+3,
∴抛物线的对称轴为x=$\frac{1}{2}$,
设对称轴交x轴于点E,则E($\frac{1}{2}$,0),
∵AB=5,
∴AE=BE=$\frac{5}{2}$,
∴A(-2,0),B(3,0),
∴4a+2a+3=0,
∴a=$\frac{1}{2}$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3,
(2)如图2,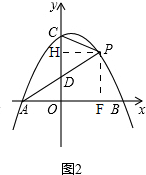
过P作PF⊥x轴于点F,作PH⊥y轴于H,
∴∠APH=∠PAB,
∵∠APC=2∠PAB,
∴∠APH=∠CPH=∠PAB,
∴tan∠CPH=tan∠PAB,
∴$\frac{CH}{PH}=\frac{PF}{AF}$,
设P(t,-$\frac{1}{2}$t2+$\frac{1}{2}$t+3),
∴$\frac{3-(-\frac{1}{2}{t}^{2}+\frac{1}{2}t+3)}{t}$=$\frac{-\frac{1}{2}{t}^{2}+\frac{1}{2}t+3}{t+2}$,
∴t=-2(舍)或t=2,
∴P(2,2),
(3)如图3,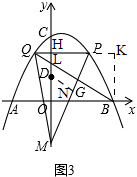
由(2)有,D(0,1),
过B作BK⊥PH于K,过D作DN⊥PM于N,
∵P(2,2),H(0,2),B(3,0),
∴PH=BK=2,DH=PK=1,∠K=∠PHD=90°,
∴△PHD≌△BKP,
∴DP=BP,
∵∠DPB=90°,
∴△DNP≌△PGB,
∴DN=PG,
∵PQ=DM,∠PGQ=∠DNM=90°,
∴RT△PGQ≌RT△DNM
∴∠PQG=∠DMN,
∵∠DMN=∠OBH,
∴∠PQG=∠OBH,
∴PQ∥x轴,
∴Q的纵坐标为2,
∴-$\frac{1}{2}$x2+$\frac{1}{2}$x+3=2,
∴x=2(舍)或x=-1,
∴Q(-1,2),
设BQ交y轴于点L,
∵B(3,0),
∴直线BQ的解析式为y=-$\frac{1}{2}$x+$\frac{3}{2}$,
∴L(0,$\frac{3}{2}$),
∴DL=$\frac{1}{2}$,
∵MD=PQ=3,
∴ML=$\frac{7}{2}$,
∴tan∠PMQ=$\frac{QG}{MG}=\frac{MN}{MG}=\frac{MD}{ML}$=$\frac{3}{\frac{7}{2}}$=$\frac{6}{7}$.
点评 此题是二次函数综合题,主要考查了待定系数法,全等三角形的性质和判定,锐角三角函数,解本题的关键是求出点P坐标,用方程的思想解决问题是本题的难点.


科目:初中数学 来源: 题型:选择题
 如图,已知等边△ABC和等边△PAF,过P作PE⊥AC于E,Q为BC延长线上一点,连接PQ交AC边于D,当PA=CQ,AB=1时,DE的长( )
如图,已知等边△ABC和等边△PAF,过P作PE⊥AC于E,Q为BC延长线上一点,连接PQ交AC边于D,当PA=CQ,AB=1时,DE的长( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$(x+y) | B. | $\frac{a}{3}$ | C. | $\frac{2}{x-y}$ | D. | $\frac{xy}{π}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.34}$ | B. | $\sqrt{\frac{2}{5}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{7a{b}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com