
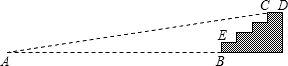
 某商场门前的台阶截面如图所示.已知每级台阶的高度(如BE)均为0.2米.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前最高点C的距离.(精确到0.1米).
某商场门前的台阶截面如图所示.已知每级台阶的高度(如BE)均为0.2米.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前最高点C的距离.(精确到0.1米).科目:初中数学 来源: 题型:
 其中一个门的门前台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角为9度.请计算从斜坡起点A到台阶前的点B的水平距离.
其中一个门的门前台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角为9度.请计算从斜坡起点A到台阶前的点B的水平距离.查看答案和解析>>
科目:初中数学 来源: 题型:
 阶前的点B的水平距离=
阶前的点B的水平距离=查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏南通卷)数学(解析版) 题型:解答题
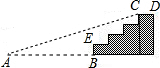
某商场门前的台阶截面如图所示.已知每级台阶的宽度(如CD)均为30cm,高度(如BE)均为20cm.为了方便残疾人行走,商场决定将其中一个门的门前台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角为9°.请计算从斜坡起点A到台阶前的点B的水平距离.(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16)

查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(38):7.6 锐角三角函数的简单应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com