
 如图,△ABC中,点D为BC中点,点E为AD中点,点F为CE中点,若S△ABC=10cm2,则S△BEF=2.5cm2.
如图,△ABC中,点D为BC中点,点E为AD中点,点F为CE中点,若S△ABC=10cm2,则S△BEF=2.5cm2. 分析 由于D、E、F分别为BC、AD、CE的中点,可判断出AD、BE、CE、BF为△ABC、△ABD、△ACD、△BEC的中线,根据中线的性质可知将相应三角形分成面积相等的两部分,据此即可解答.
解答 解:∵由于D、E、F分别为BC、AD、CE的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
S△BEC=$\frac{1}{2}$S△ABC=5cm2.
S△BEF=$\frac{1}{2}$S△BEC=2.5cm2.
解法2:∵D是BC的中点
∴S△ABD=S△ADC(等底等高的三角形面积相等),
∵E是AD的中点,
∴S△ABE=S△BDE,S△ACE=S△CDE(等底等高的三角形面积相等),
∴S△ABE=S△DBE=S△DCE=S△AEC,
∴S△BEC=$\frac{1}{2}$S△ABC=5cm2.
∵F是CE的中点,
∴S△BEF=S△BCE,
∴S△BEF=$\frac{1}{2}$S△BEC=2.5cm2.
故答案为2.5
点评 此题考查了三角形的面积,根据三角形中线将三角形的面积分成相等的两部分解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
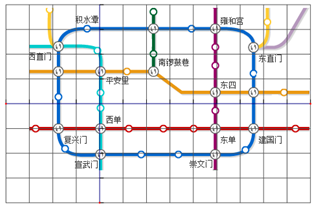 如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )
如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )| A. | (0,5) | B. | (5,0) | C. | (0,-5) | D. | (-5,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
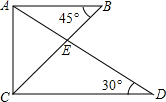 将一副三角尺如图所示叠放在一起,则$\frac{BE}{EC}$的值是( )
将一副三角尺如图所示叠放在一起,则$\frac{BE}{EC}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
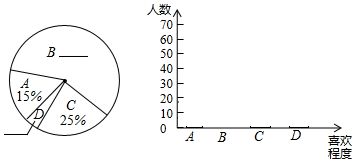 某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表. | 喜欢程度 | 频数 |
| A | 18 |
| B | 66 |
| C | 30 |
| D | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com