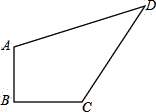
【题目】如图，一块草坪的形状为四边形ABCD，其中∠B＝90°，AB＝3m，BC＝4m，CD＝12m，AD＝13m，求这块草坪的面积。
【答案】这块草坪的面积为36平方厘米．
【解析】试题
如下图，连接AC，由已知条件根据勾股定理可得AC=5，结合CD=12，AD=13，由勾股定理逆定理可得∠ACD=90°，这样由四边形ABCD是由两个直角三角形构成的即可求出其面积了.
试题解析：
连接AC，
∵在Rt△ABC中，∠B=90°，AB=3，BC=4，
∴AC=5，
∵（AC）2+（CD）2=25+144=169，（AD）2=（13）2=169
∴（AC）2+（CD）2=（AD）2，
∴∠ACD=90°，即△ACD是直角三角形，
∴草坪面积=
S△ABC+S△ACD=×3×4+×5×12=6+30=36．
即这块草坪的面积为36平方厘米．
科目：初中数学 来源： 题型：
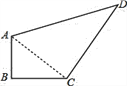
【题目】已知：PA=
，PB＝4，以AB为一边作正方形ABCD，使P、D两点落在直线AB的两侧．
(1)如图，当∠APB＝45°时，求AB及PD的长；
(2)当∠APB变化，且其它条件不变时，求PD的最大值，及相应∠APB的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，AB=10，BC=12，E为DC的中点，连接BE，作AF⊥BE，垂足为F．
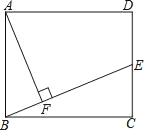
（1）求证：△BEC∽△ABF；
（2）求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A．了解飞行员视力的达标率应使用抽样调查
B．一组数据3，6，6，7，9的中位数是6
C．从2000名学生中选200名学生进行抽样调查，样本容量为2000
D．一组数据1，2，3，4，5的方差是10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解2014届某校男生报考泉州市中考体育测试项目的意向，某校课题研究小组从毕业年段各班男生随机抽取若干人组成调查样本，根据收集整理到的数据绘制成以下不完全统计图.根据以上信息，解答下列问题：
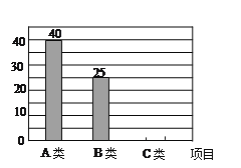
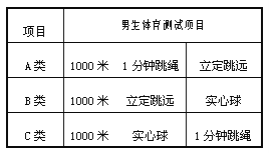
（1）该小组采用的调查方式是____________，被调查的样本容量是_______；
（2）请补充完整图中的条形统计图和扇形统计图（请标上百分率）（百分率精确到1%）；
（3）该校共有600名初三男生，请估计报考A类的男生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．阜阳市某家快递公司，2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月投递的快递总件数的增长率相同．
(1)求该快递公司投递快递总件数的月平均增长率？
(2) 如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一只不透明的布袋中装有红球 3 个、黄球 1 个，这些球除颜色外都相同，均匀摇匀．
(1)从布袋中一次摸出 1 个球，计算“摸出的球恰是黄球”的概率；
(2)从布袋中一次摸出 2 个球，计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线l与x轴相交于点M（3，0），与y轴相交于点N（0，4），点A为MN的中点，反比例函数y=
（x＞0）的图象过点A．
（1）求直线l和反比例函数的解析式；
（2）在函数y=
（k＞0）的图象上取异于点A的一点C，作CB⊥x轴于点B，连接OC交直线l于点P，若△ONP的面积是△OBC面积的3倍，求点P的坐标．
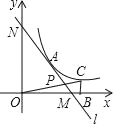
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ABC为直角，以AB为直径作⊙O交AC于点D，点E为BC中点，连结DE，DB.
（1）求证：DE与⊙O相切；
（2）若∠C＝30°，求∠BOD的度数；
（3）在（2）的条件下，若⊙O半径为2， 求阴影部分面积．
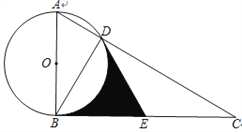
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com