
如图,D、A、E在一条直线上,△A DC≌△AEB,∠BAC= 40°,∠D= 45°
DC≌△AEB,∠BAC= 40°,∠D= 45°
求:(1)∠B的度数;
( 2)∠BMC
2)∠BMC 的度数.
的度数.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
植树 节前夕,某林场组织20辆汽车装运芒果树、木棉树和垂叶榕三种树木共100棵来深圳销售.按计划20辆车都要装运,每辆汽车只能装运同一种树木,且必须装满.根据表格提供的信息,解答下列问题.
节前夕,某林场组织20辆汽车装运芒果树、木棉树和垂叶榕三种树木共100棵来深圳销售.按计划20辆车都要装运,每辆汽车只能装运同一种树木,且必须装满.根据表格提供的信息,解答下列问题.
(1)设装运芒果树的车辆数为 ,装运木棉树的车辆数为
,装运木棉树的车辆数为 ,求
,求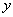 与
与 之间的函数关系式;(3分)
之间的函数关系式;(3分)
(2)如果安排装运芒果树的车辆数不少于5辆,装运木棉树的车辆数不少于6辆,那么车辆的安排有几种方案?并写出每种安排方案?(3分)
(3)若要求总运费最少,应采用(2)中哪种安排方案?并求出最少总运费?(3分)
| 树木种类 | 芒果树 | 木棉树 | 垂叶榕 |
| 每辆汽车运载量(棵) | 6 | 5 | 4 |
| 平均每棵树运费(元) | 120 | 160 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在学习了利用尺规作一个角的平分线后,爱钻研的小明发现,只用一把刻度尺也可以作出一个角的平分线.他是这样作的(如图).
(1)分别在∠AOB的两边OA,OB上各取一点C,D,使得OC=OD;
(2)连接CD,并量出CD的长度,取CD的中点E;
(3)过O,E两点作射线.则OE就是∠AOB的平分线.
你认为小明的想法正确吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
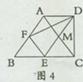
如图4,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )
A.△ABC是等腰三角形 B.四边形EFAM是菱形
C.S△BEF=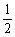 S△ACD D.DE平分∠CDF
S△ACD D.DE平分∠CDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com