
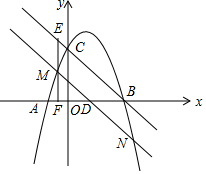
 如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,分析 (1)在y=-x2+2x+3中,令y=0可求得A、B的坐标,令x=0可求得C点坐标;
(2)由B、C的坐标可求得直线BC的解析式,设M(t,-t2+2t+3),则可表示出E点坐标,可用t表示出MF和EF的长,由M为EF的中点可得到关于t的方程,则可求得EF的长,即可得出BF的长,可求得BD的长;
(3)过D作DH∥EF,则可证得四边形DHEM为平行四边形,则可知S2-S1=S△HDB,则可求得答案.
解答 解:
(1)在y=-x2+2x+3中,令y=0可得-x2+2x+3=0,解得x=-1或x=3,
∴A(-1,0),B(3,0),
令x=0可得y=3,
∴C(0,3);
(2)∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3,
∵点M是抛物线上A,C之间的一个动点,
∴可设M(t,-t2+2t+3)(-1<t<0),则E(t,-t+3),
∴EF=-t+3,MF=-t2+2t+3,
∵M为EF的中点,
∴-t+3=2(-t2+2t+3),解得t=-$\frac{1}{2}$或t=3(不符合题意,舍去),
∴F(-$\frac{1}{2}$,0),
∴BF=3-(-$\frac{1}{2}$)=$\frac{7}{2}$,
∵MN∥BC,
∴D为BF的中点,
∴BD=$\frac{1}{2}$BF=$\frac{7}{4}$;
(3)如图,过D作DH∥EF,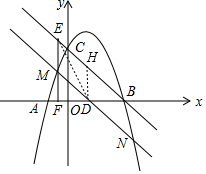
∵MN∥BC,
∴四边形DHEM为平行四边形,
∴S△DEM=S△DEH,
∵DH⊥BD,且∠OBC=45°,
∴DH=BD=1,
∴S2-S1=S△HDB=$\frac{1}{2}$BD•DH=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题为二次函数的综合应用,涉及待定系数法、抛物线与坐标轴的交点、三角形中位线定理、平行四边形的判定和性质、三角形的面积等知识.在(2)中用M点的坐标分别表示出MF和EF的长是解题的关键,在(3)中得出S2-S1=S△HDB是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
| A. | 每位考生的数学成绩是个体 | B. | 近35000名考生是总体 | ||
| C. | 这1000名考生是总体的一个样本 | D. | 1000名考生是样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+2<b+2 | B. | a-2<b-2 | C. | $\frac{a}{2}$>$\frac{b}{2}$ | D. | -2a>-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不等式-2x>4的两边同时除以-2,得x>2 | |
| B. | 不等式1-x>3的两边同时减去1,得x>2 | |
| C. | 不等式4x-2<3-x移项,得4x+x<3-2 | |
| D. | 不等式$\frac{x}{3}$<1-$\frac{x}{2}$去分母,得2x<6-3x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
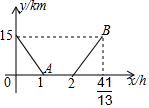 小华家距离县城15km,星期天8:00,小华骑自行车从家出发,到县城购买学习用品,小华与县城的距离y(km)与骑车时间x(h)之间的关系如图所示,给出以下结论:①小华骑车到县城的速度是15km/h;②小华骑车从县城回家的速度是13km/h;③小华在县城购买学习用品用了1h;④B点表示经过$\frac{41}{13}$h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有( )
小华家距离县城15km,星期天8:00,小华骑自行车从家出发,到县城购买学习用品,小华与县城的距离y(km)与骑车时间x(h)之间的关系如图所示,给出以下结论:①小华骑车到县城的速度是15km/h;②小华骑车从县城回家的速度是13km/h;③小华在县城购买学习用品用了1h;④B点表示经过$\frac{41}{13}$h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知两个完全相同的大长方形,长为a,各放入四个完全一样的白色小长方形后,得到图(1)、图(2),那么,图(1)阴影部分的周长与图(2)阴影部分的周长的差是( )(用含a的代数式表示)
已知两个完全相同的大长方形,长为a,各放入四个完全一样的白色小长方形后,得到图(1)、图(2),那么,图(1)阴影部分的周长与图(2)阴影部分的周长的差是( )(用含a的代数式表示)| A. | $\frac{1}{2}$a | B. | $\frac{3}{4}$a | C. | a | D. | $\frac{5}{4}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com