
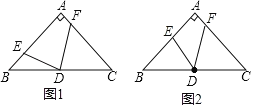
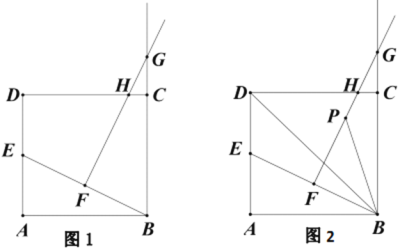
【题目】已知:△ABC,AB=AC,∠BAC=90°,点D是边BC的中点,点E在边AB上(点E不与点A、B重合),点F在边AC上,联结DE、DF.
(1)如图1,当∠EDF=90°时,求证:BE=AF;
(2)如图2,当∠EDF=45°时,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接AD,证△BDE≌△ADF(ASA),即可得出结论;
(2)证明△BDE∽△CFD.得出![]() ,得出
,得出![]() ,由BD=CD,即可得出结论.
,由BD=CD,即可得出结论.
(1)连接AD,如图1所示:
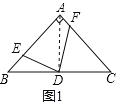
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°.
∵点D是边BC的中点,
∴AD![]() BC=BD,AD⊥BC,∠BAD=∠CAD=45°,
BC=BD,AD⊥BC,∠BAD=∠CAD=45°,
∴∠B=∠CAD.
∵∠EDF=90°,
∴∠ADF+∠ADE=90°
∵∠BDE+∠ADE=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中, ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF;
(2)∵∠BDF=∠BDE+∠EDF,∠BDF=∠C+∠CFD,
∴∠BDE+∠EDF=∠C+∠CFD.
又∵∠C=∠EDF=45°,
∴∠BDE=∠CFD,
∴△BDE∽△CFD,
∴![]() ,
,
∴![]() ,
,
又∵BD=CD,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一不透明的袋子中装有四张标有数字![]() 的卡片,这些卡片除数字外其余均相同.小明同学按照一定的规则抽出两张卡片,并把卡片上的数字相加,下图是他所画的树状图的一部分.
的卡片,这些卡片除数字外其余均相同.小明同学按照一定的规则抽出两张卡片,并把卡片上的数字相加,下图是他所画的树状图的一部分.
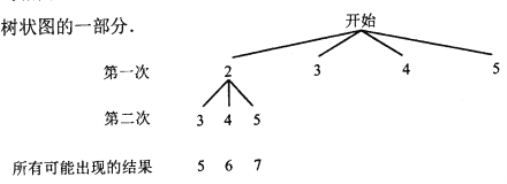
(1)由上图分析,该游戏规则是:第一次从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),第二次随机再抽出一张卡片;
(2)帮小明同学补全树状图,并求小明同学两次抽到卡片上的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
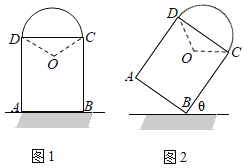
【题目】图1为一艺术拱门,下部为矩形ABCD,AB、AD的长分别为![]() m和4m,上部是圆心为O的劣弧CD,∠COD=120°.现欲以点B为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2所示.设BC与地面水平线所成的角为
m和4m,上部是圆心为O的劣弧CD,∠COD=120°.现欲以点B为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2所示.设BC与地面水平线所成的角为![]() ,记拱门上的点到地面的距离为h,当h取最大值时,此时
,记拱门上的点到地面的距离为h,当h取最大值时,此时![]() 为________°.
为________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AD=2,AB=a,点E为AD的中点,连接BE.过BE的中点F作FG⊥BE,交射线BC于点G,交边CD于H点.
(1)连接HE、HB
①求证:HE=HB;
②若a=4,求CH的长.
(2)连接EG,△BEG面积为S
①BE= (用含a的代数式表示);
②求S与a的函数关系式.
(3)如图2,设FG的中点为P,连接PB、BD.猜想∠GBP与∠DBE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
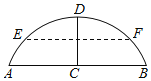
【题目】如图,有一拱桥的桥拱是圆弧形,已知桥拱的水面跨度AB(弧所对的弦的长)为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求桥拱所在圆的半径长;
(2)如果水面AB上升到EF时,从点E测得桥顶D的仰角为α,且cotα=3,求水面上升的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
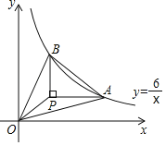
【题目】如图,A、B是函数y=![]() 上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
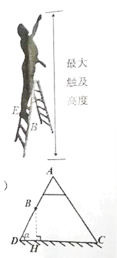
【题目】某电工想换房间的灯泡,已知灯泡到地面的距离为![]() ,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,
,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,![]() .设梯子一边
.设梯子一边![]() 与地面的夹角为
与地面的夹角为![]() ,且
,且![]() 可调节的范围为
可调节的范围为![]() .当
.当![]() 时,电工站在梯子安全挡中最高一档踏板
时,电工站在梯子安全挡中最高一档踏板![]() 上的最大触及高度为
上的最大触及高度为![]() .
.
(1)当![]() 时,求踏板
时,求踏板![]() 离地面的高度
离地面的高度![]() .(精确到
.(精确到![]() )
)
(2)调节角度,试判断电工是否可以换下灯泡,并说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com