
 一只蚂蚁在立方体的表面积爬行.
一只蚂蚁在立方体的表面积爬行. ,进而得出答案即可;
,进而得出答案即可; 解:(I)如图1所示,沿线段AB爬行即可,根据两点之间线段最短;
解:(I)如图1所示,沿线段AB爬行即可,根据两点之间线段最短;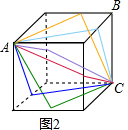
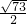 cm,图②中AE=
cm,图②中AE= cm.
cm.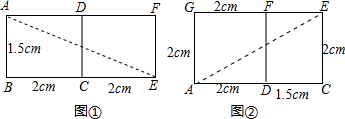


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
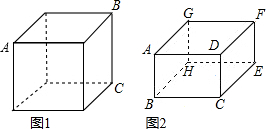 一只蚂蚁在立方体的表面积爬行.
一只蚂蚁在立方体的表面积爬行.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com