
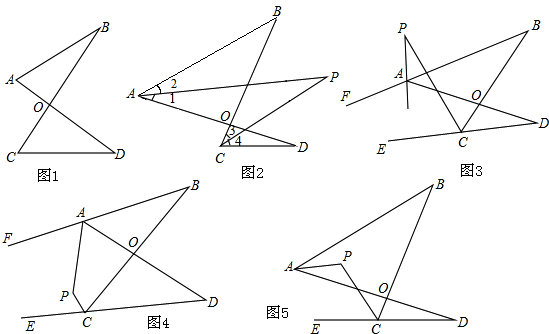
分析 (1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
②根据四边形的内角和等于360°可得(180°-∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°-∠3)+∠D=360°,然后整理即可得解;
③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.
解答 解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①∠P=26゜.
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4
由(1)的结论得:∠PAD+∠P=∠PCD+∠D ①,∠PAB+∠P=∠PCB+∠B ②,
∵∠PAB=∠1,∠1=∠2,
∴∠PAB=∠2,
∴∠2+∠P=∠3+∠B ③,
①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P=$\frac{1}{2}($∠B+∠D )=26°.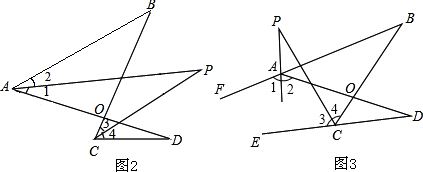
②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°-2∠1)+∠B=(180°-2∠4)+∠D,
在四边形APCB中,(180°-∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°-∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°-$\frac{1}{2}$(∠B+∠D);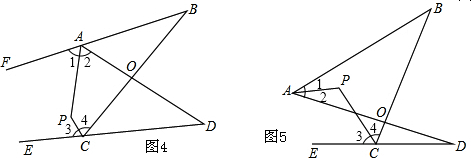
③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∵(∠1+∠2)+∠B=(180°-2∠3)+∠D,
∠2+∠P=(180°-∠3)+∠D,
∴2∠P=180°+∠D+∠B,
∴∠P=90°+$\frac{1}{2}$(∠B+∠D).
点评 本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
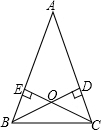 如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.
如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
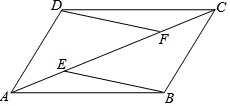 已知:如图,AD∥BC,AD=BC,E、F是四边形ABCD的对角线AC上的两点,并且AE=CF,
已知:如图,AD∥BC,AD=BC,E、F是四边形ABCD的对角线AC上的两点,并且AE=CF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com