
【题目】2017年国庆节期间,南宁动物园在7天假期中每天接待游客的人数与前一天相比的变化情况(正数表示比前一天多的人数,负数表示比前一天少的人数)如下表:
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化/万人 | +1.7 | +0.6 | +0.3 | -0.3 | -0.6 | +0.2 | -1.1 |
(1) 请判断七天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(2) 若9月30日的游客人数为3万人,求这7天的游客总人数是多少万人?
【答案】(1)游客人数最多的为3日,最少的为7日,这两天的游客人数相差2.6-0.8=1.4(万人);
(2)这7天的游客总人数是34.3万人.
【解析】分析:(1)由表知,从10月4日旅游的人数比前一天少,所以10月3日人数最多;10月7日人数最少;10月3日人数减去10月7日人数可得它们相差的人数;
(2)在9月30日的游客人数为3万人的基础上,把黄金周期间这七天的人数先分别求出来,再分别相加即可.
本题解析:
(1)10月1日至7日每天游客与9月30日相比的变化情况是:
1日:+1.7(万人)
2日:1.7+0.6=2.3(万人)
3日:2.3+0.3=2.6(万人)
4日:2.6-0.3=2.3(万人)
5日:2.3-0.6=1.7(万人)
6日:1.7+0.2=1.9(万人)
7日:1.9-1.1=0.8(万人)
所以游客人数最多的为3日,最少的为7日,这两天的游客人数相差2.6-0.8=1.4(万人).
(2)法1:这七天的游客人数分别为
1日:3+1.7=4.7(万人)
2日:4.7+0.6=5.3(万人)
3日:5.3+0.3=5.6(万人)
4日:5.6-0.3=5.3(万人)
5日:5.3-0.6=4.7(万人)
6日:4.7+0.2=4.9(万人)
7日:4.9-1.1=3.8(万人)
总人数:4.7+5.3+5.6+5.3+4.7+4.9+3.8=34.3(万人)
答:这7天的游客总人数是34.3万人.
法2: ![]() (万人)
(万人)
答:这7天的游客总人数是34.3万人


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
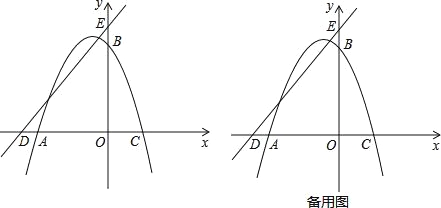
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图ΔABC中,∠B =∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是( )
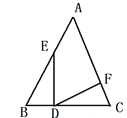
A. 2α+∠A=90° B. 2α+∠A=180°
C. α+∠A=90° D. α+∠A=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
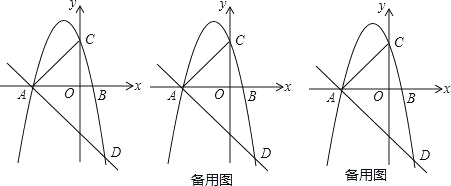
【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣![]() x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒![]() 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com