[题目]如图7-①.图7-②.图7-③.图7-④.-.是用围棋棋子按照某种规律摆成的一行“广字.按照这种规律.第5个“广字中的棋子个数是 .第个“广字中的棋子个数是题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图7-①，图7-②，图7-③，图7-④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是________，第个“广”字中的棋子个数是________

【答案】15 2n+5

【解析】

通过观察，找到图形中的规律，即可得到答案.

解：由题目得：第1个“广”字中的棋子个数是7；

第2个“广”字中的棋子个数是：7+(21)×2=9；

第3个“广”字中的棋子个数是：7+(31)×2=11；

第4个“广”字中的棋子个数是：7+(41)×2=13；

∴第5个“广”字中的棋子个数是：7+(51)×2=15；

进一步发现规律：第n个“广”字中的棋子个数是：7+(n1)×2=2n+5.

故答案为：15，2n+5.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】先阅读一段文字，再回答下列问题：

已知在平面内两点坐标P1(x1，y1)，P2(x2，y2)，其两点间距离公式为，同时，当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴距离公式可简化成|x2-x1|或|y2-y1|．

(1)已知A(3，5)，B(-2，-1)，试求A，B两点的距离；

(2)已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为-1，试求A，B两点的距离．

(3)已知一个三角形各顶点坐标为A(0，6)，B(-3，2)，C(3，2)，你能断定此三角形的形状吗?说明理由。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）画出△ABC关于y轴的对称图形,其中A、B、C的对应点分别为，，

（2）= .

（3）画出以为腰的等腰△CAD，点D在y轴右侧的小正方形的顶点上，且△CAD的面积为6 .

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，已知O为坐标原点，长方形ABCD（点A与坐标原点重合）的顶点D、B分别在x轴、y轴上，且点C的坐标为（-4，8），连接BD，将△ABD沿直线BD翻折至△ABD，交CD于点E．

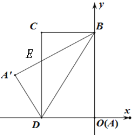
（1）求S△BED的面积；

（2）求点A坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．

（1）如图1，若BD=BA，求证：△ABE≌△DBE；

（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AFAC．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】黑板上写有1，2，3，…，2019，2020这2020个自然数，对它们进行操作，每次操作规则如下：擦掉写在黑板上的三个数后，再添写上所擦掉三个数之和的个位数字，例如：擦掉5，13和2010后，添加上8；若再擦掉8，8，38，添上4，等等.如果经过1004次操作后，发现黑板上剩下两个数，一个是29，求另一个数.