
【题目】水果店张阿姨以每斤2元的利润出售一种水果,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.2元,每天可多售出40斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是________斤(用含x的代数式表示);
(2)销售这种水果要想每天赢利300元,张阿姨需将这种水果每斤的售价降低多少元?
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(
边上的动点(![]() 不与
不与![]() 、
、![]() 重合),
重合),![]()

![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)![]() 与
与![]() 的大小关系为________.请证明你的结论;
的大小关系为________.请证明你的结论;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(4)是否存在![]() ,使
,使![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍?若存在,求出
倍?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=![]() ,BC=6cm,AC=10cm。
,BC=6cm,AC=10cm。
(1)求AB的长;
(2)若P点从点B出发,以2cm/s的速度在BC所在的直线![]() 上运动,设运动时间为t秒,那么当t为何值时,△ACP为等腰三角形。
上运动,设运动时间为t秒,那么当t为何值时,△ACP为等腰三角形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
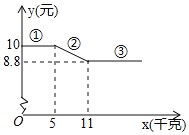
【题目】某水果店进行了一次水果促销活动,在该店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图所示,
(1)当0<x≤5时,单价y为 元.当单价y=8.8时,x的取值范围为 .
(2)根据函数图象,求第②段函数图象中单价y(元)与购买量(千克)的函数关系式,并写出x的取值范围.
(3)促销活动期间,张老师计划去该店购买A种水果10千克,那么张老师共需花费多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 ![]() cm?
cm?
(3)经过几秒,![]() 的面积等于
的面积等于![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com