
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±ĻßAC£ŗy£½©3x+3![]() ÓėÖ±ĻßAB£ŗy£½ax+b½»ÓŚµćA£¬ĒŅB£Ø©9£¬0£©£®
ÓėÖ±ĻßAB£ŗy£½ax+b½»ÓŚµćA£¬ĒŅB£Ø©9£¬0£©£®
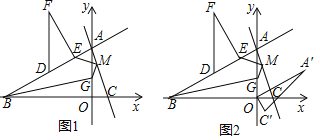
£Ø1£©ČōFŹĒµŚ¶žĻóĻŽĪ»ÓŚÖ±ĻßABÉĻ·½µÄŅ»µć£¬¹żF×÷FE”ĶABÓŚE£¬¹żF×÷FD”ĪyÖį½»Ö±ĻßABÓŚD£¬DĪŖABÖŠµć£¬ĘäÖŠ”÷DFFµÄÖܳ¤ŹĒ12+4![]() £¬ČōMĪŖĻ߶ĪACÉĻŅ»¶Æµć£¬Į¬½ÓEM£¬ĒóEM+
£¬ČōMĪŖĻ߶ĪACÉĻŅ»¶Æµć£¬Į¬½ÓEM£¬ĒóEM+![]() MCµÄ×īŠ”Öµ£¬“ĖŹ±yÖįÉĻÓŠŅ»øö¶ÆµćG£¬µ±|BG©MG|×ī“óŹ±£¬ĒóGµć×ų±ź£»
MCµÄ×īŠ”Öµ£¬“ĖŹ±yÖįÉĻÓŠŅ»øö¶ÆµćG£¬µ±|BG©MG|×ī“óŹ±£¬ĒóGµć×ų±ź£»
£Ø2£©ŌŚ£Ø1£©µÄĒéæöĻĀ£¬½«”÷AOCČĘOµćĖ³Ź±ÕėŠż×Ŗ60”ćŗóµĆµ½”÷A”äOC'£¬ČēĶ¼2£¬½«Ļ߶ĪOA”äŃŲ×ÅxÖįĘ½ŅĘ£¬¼ĒĘ½ŅĘ¹ż³ĢÖŠµÄĻ߶ĪOA”äĪŖO”äA”壬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌµćO”䣬A”壬E£¬PĪŖ¶„µćµÄĖıߊĪĪŖĮāŠĪ£¬Čō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() -
-![]() £¬£Ø0£¬
£¬£Ø0£¬![]() £©£»£Ø2£©“ęŌŚ£¬£Ø2
£©£»£Ø2£©“ęŌŚ£¬£Ø2![]() £¬2+3
£¬2+3![]() £©»ņ£Ø
£©»ņ£Ø![]() ©9£¬2£©»ņ£Ø6
©9£¬2£©»ņ£Ø6![]() ©3£¬©2£©
©3£¬©2£©
”¾½āĪö”æ
£Ø1£©µć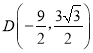 £¬Ōņµć
£¬Ōņµć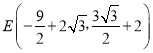 £¬¹żµćC×÷xÖįµÄ“¹Ļß”¢¹żµćM×÷yÖįµÄ“¹Ļߣ¬Į½“¹Ļß½»ÓŚµćH£¬MH£½MCcos¦Į£½
£¬¹żµćC×÷xÖįµÄ“¹Ļß”¢¹żµćM×÷yÖįµÄ“¹Ļߣ¬Į½“¹Ļß½»ÓŚµćH£¬MH£½MCcos¦Į£½![]() MC£¬µ±µćE”¢M”¢HČżµć¹²Ļߏ±£¬EM+MH£½EM+
MC£¬µ±µćE”¢M”¢HČżµć¹²Ļߏ±£¬EM+MH£½EM+![]() MC×īŠ”£¬µć
MC×īŠ”£¬µć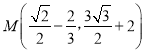 £¬EM+
£¬EM+![]() MC×īŠ”Öµ£½EH£½xC©xE£½
MC×īŠ”Öµ£½EH£½xC©xE£½![]() £»×÷µćM¹ŲÓŚyÖįµÄ¶Ō³Ęµć
£»×÷µćM¹ŲÓŚyÖįµÄ¶Ō³Ęµć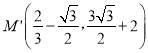 £¬Į¬½ÓBM”ä½»yÖįÓŚµćG£¬Ōņ“ĖŹ±|BG©MG|×ī“󣬼“æÉĒó½ā£»
£¬Į¬½ÓBM”ä½»yÖįÓŚµćG£¬Ōņ“ĖŹ±|BG©MG|×ī“󣬼“æÉĒó½ā£»
£Ø2£©ÉčĻ߶ĪOA”äŃŲ×ÅxÖįĘ½ŅĘĮĖmøöµ„Ī»£¬ŌņµćO”䔢A”åµÄ×ų±ź·Ö±šĪŖ£Øm£¬0£©”¢(![]() £¬
£¬![]() )£¬¶ųµć
)£¬¶ųµć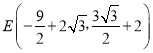 £¬
£¬
¢Łµ±O”äA”åŹĒĮāŠĪµÄ±ßŹ±£¬ŌņEP£ØP”䣩£½O”äA”壽OA£½3![]() £¬¼“æÉĒó½ā£»
£¬¼“æÉĒó½ā£»
¢Śµ±O”äA”åŹĒĮāŠĪµÄ¶Ō½ĒĻߏ±£¬ÉčµćP£Øa£¬b£©£¬ÓÉÖŠµć¹«Ź½µĆ£ŗ![]() £¬
£¬![]() £¬¶ųEO£½EA£¬¼“£ŗ
£¬¶ųEO£½EA£¬¼“£ŗ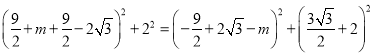 £¬¼“æÉĒó½ā£®
£¬¼“æÉĒó½ā£®
£Ø1£©ÓÉAC£ŗ![]() µĆ£ŗµćA”¢CµÄ×ų±ź·Ö±šĪŖ£ŗ
µĆ£ŗµćA”¢CµÄ×ų±ź·Ö±šĪŖ£ŗ![]() £¬
£¬
”ą![]() £¬
£¬![]()
Ōņ![]() £¬Ōņ
£¬Ōņ![]()
µć![]() £¬µćA
£¬µćA![]() £¬“śČėy£½ax+b£¬
£¬“śČėy£½ax+b£¬
µĆ£ŗ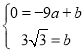 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ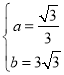
ŌņÖ±ĻßABµÄ±ķ“ļŹ½ĪŖ£ŗ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
”ßFE”ĶAB£¬FD”ĪyÖį£¬Ōņ”ĻF£½”ĻABO£½30”ć£¬
Éč£ŗ![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬![]() £¬”÷DFFµÄÖܳ¤ŹĒ
£¬”÷DFFµÄÖܳ¤ŹĒ![]() £¬
£¬
Ōņ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬
DĪŖABÖŠµć£¬Ōņµć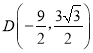 £¬
£¬
s£½ED£½4£¬Ōņ![]() £¬
£¬
Ōņµć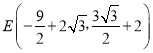 £¬
£¬
¹żµćC×÷xÖįµÄ“¹Ļß”¢¹żµćM×÷yÖįµÄ“¹Ļߣ¬Į½“¹Ļß½»ÓŚµćH£¬ČēĶ¼1£ŗ
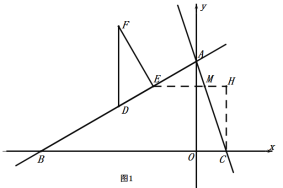
Ōņ”ĻHMC£½”ĻACO£½¦Į£¬ŌņMH£½MCcos¦Į£½![]() MC£¬
MC£¬
µ±µćE”¢M”¢HČżµć¹²Ļߏ±£¬EM+MH£½EM+![]() MC×īŠ”£¬
MC×īŠ”£¬
Ōņ![]() £¬
£¬
µćMŌŚÖ±ĻßACÉĻ£¬Ōņµć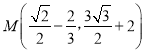 £¬
£¬
×÷µćM¹ŲÓŚyÖįµÄ¶Ō³Ęµć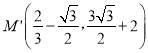 £¬Į¬½ÓBM”ä½»yÖįÓŚµćG£¬ČēĶ¼2£ŗ
£¬Į¬½ÓBM”ä½»yÖįÓŚµćG£¬ČēĶ¼2£ŗ
ŌņµćGĪŖĖłĒ󣬓ĖŹ±|BG©MG|×ī“ó£¬
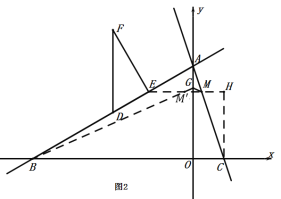
½«![]() ”¢
”¢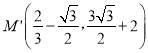 µÄ×ų±ź“śČėŅ»“ĪŗÆŹż±ķ“ļŹ½£ŗy£½kx+b£¬
µÄ×ų±ź“śČėŅ»“ĪŗÆŹż±ķ“ļŹ½£ŗy£½kx+b£¬
½āµĆ£ŗ![]()
¹ŹµćGµÄ×ų±źĪŖ£ŗ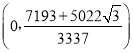 £»
£»
×ŪÉĻ£¬EM+![]() MC×īŠ”ÖµĪŖ£ŗ
MC×īŠ”ÖµĪŖ£ŗ![]() ©
©![]() £¬GµÄ×ų±źĪŖ£ŗ£Ø0£¬
£¬GµÄ×ų±źĪŖ£ŗ£Ø0£¬![]() £©£»
£©£»
£Ø2£©½«”÷AOCČĘOµćĖ³Ź±ÕėŠż×Ŗ60”ćŗóµĆµ½”÷A”äOC'£¬
Ōņ”÷OAA”äĪŖ±ß³¤ĪŖ4µÄµČ±ßČż½ĒŠĪ£¬ŌņµćA”ä£Ø![]() £¬
£¬![]() £©£¬
£©£¬
ÉčĻ߶ĪOA”äŃŲ×ÅxÖįĘ½ŅĘĮĖmøöµ„Ī»£¬
ŌņµćO”䔢A”åµÄ×ų±ź·Ö±šĪŖ£Øm£¬0£©”¢£Ø![]() £¬
£¬![]() £©£¬¶ųµć
£©£¬¶ųµć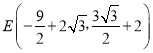 £¬
£¬
¢Łµ±O”äA”åŹĒĮāŠĪµÄ±ßŹ±£¬
Ö±ĻßOA”äŗĶÖ±ĻßABµÄĒ抱½Ē¶¼ŹĒ30”ć£¬¹ŹO”äA”å”ĪOA”ä”ĪAB£¬
ŌņEP£ØP”䣩£½O”äA”壽OA£½3![]() £¬
£¬
ŌņxP©xE£½3![]() cos30”ć£½
cos30”ć£½![]() £¬
£¬
¹ŹµćP£Ø2![]() £¬2+3
£¬2+3![]() £©£¬
£©£¬
Ķ¬ĄķµćP”ä£Ø![]() £¬2£©£»
£¬2£©£»
¢Śµ±O”äA”åŹĒĮāŠĪµÄ¶Ō½ĒĻߏ±£¬
ÉčµćP£Øa£¬b£©£¬
ÓÉÖŠµć¹«Ź½µĆ£ŗ![]() £¬
£¬![]() £¬
£¬
¶ųEO£½EA£¬¼“£ŗ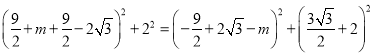 £¬
£¬
½āµĆ£ŗ![]() £¬b£½©2£¬
£¬b£½©2£¬![]() ©6£¬
©6£¬
¹Ź£ŗ![]() 6
6![]() ©3£¬
©3£¬![]() £¬
£¬
ŌņµćP£Ø6![]() ©3£¬©2£©£»
©3£¬©2£©£»
×ŪÉĻ£¬µćP×ų±źĪŖ£ŗ£Ø2![]() £¬2+3
£¬2+3![]() £©»ņ£Ø
£©»ņ£Ø![]() ©9£¬2£©»ņ£Ø6
©9£¬2£©»ņ£Ø6![]() ©3£¬©2£©£®
©3£¬©2£©£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖABĪŖ”ŃOµÄÖ±¾¶£¬CDĒŠ”ŃOÓŚCµć£¬ĻŅCF”ĶABÓŚEµć£¬Į¬½įAC£®
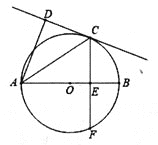
£Ø1£©ĒóÖ¤£ŗ”ĻACD=”ĻACF£»
£Ø2£©µ±AD”ĶCD£¬BE=2cm£¬CF=8cm£¬ĒóADµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
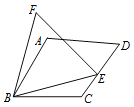
”¾ĢāÄæ”æČēĶ¼7£¬ŌŚĖıߊĪABCDÖŠ£¬AB£½BC£¬”ĻABC£½60”ć£¬EŹĒCD±ßÉĻŅ»µć£¬Į¬½ÓBE£¬ŅŌBEĪŖŅ»±ß×÷µČ±ßČż½ĒŠĪBEF.ĒėÓĆÖ±³ßŌŚĶ¼ÖŠĮ¬½ÓŅ»ĢõĻ߶Ī£¬Ź¹Ķ¼ÖŠ“ęŌŚ¾¹żŠż×ŖæÉĶźČ«ÖŲŗĻµÄĮ½øöČż½ĒŠĪ£¬²¢ĖµĆ÷ÕāĮ½øöČż½ĒŠĪ¾¹żŹ²Ć“ŃłµÄŠż×ŖæÉÖŲŗĻ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=mx2£2mx£3 (m”Ł0)ÓėyÖį½»ÓŚµćA£¬Ęä¶Ō³ĘÖįÓėxÖį½»ÓŚµćB£¬¶„µćĪŖCµć£®
£Ø1£©ĒóµćAŗĶµćBµÄ×ų±ź£»
£Ø2£©Čō”ĻACB£½45”ć£¬Ēó“ĖÅ×ĪļĻߵıķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČėŃ§æ¼ŹŌĒ°£¬Ä³ÓļĪÄĄĻŹ¦ĪŖĮĖĮĖ½āĖłČĪ½ĢµÄ¼×”¢ŅŅĮ½°ąŃ§Éś¼ŁĘŚĻņµÄÓļĪÄ»ł“”ÖŖŹ¶±³ĖŠĒéæö£¬¶ŌĮ½øö°ąµÄѧɜ½ųŠŠĮĖÓļĪÄ»ł“”ÖŖŹ¶±³ĖŠ¼ģ²ā£¬Āś·Ö100·Ö£®ĻÖ“ÓĮ½øö°ą·Ö±šĖ껜³éČ”ĮĖ20ĆūѧɜµÄ¼ģ²ā³É¼Ø½ųŠŠÕūĄķ£¬ĆčŹöŗĶ·ÖĪö£Ø³É¼ØµĆ·ÖÓĆx±ķŹ¾£¬¹²·ÖĪŖĪå×é£ŗ
A.0”Üx£¼80£¬B.80”Üx£¼85£¬C.85”Üx£¼90£¬D.90”Üx£¼95£¬E.95”Üx£¼100£©£¬ĻĀĆęøų³öĮĖ²æ·ÖŠÅĻ¢£ŗ
¼×°ą20ĆūѧɜµÄ³É¼ØĪŖ£ŗ
¼××é | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
ŅŅ°ą20ĆūѧɜµÄ³É¼ØŌŚD×éÖŠµÄŹż¾ŻŹĒ£ŗ93£¬91£¬92£¬94£¬92£¬92£¬92
¼×”¢ŅŅĮ½°ą³éČ”µÄѧɜ³É¼ØŹż¾ŻĶ³¼Ę±ķ
°ą¼¶ | ¼××é | ŅŅ×é |
Ę½¾łŹż | 91 | 92 |
ÖŠĪ»Źż | 91 | b |
ÖŚŹż | c | 92 |
·½²ī | 41.2 | 27.3 |

øł¾ŻŅŌÉĻŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ö±½ÓŠ“³öÉĻŹöĶ¼±ķÖŠa£¬b£¬cµÄÖµ£ŗa£½”” ””£»b£½”” ””£»c£½”” ””£»
£Ø2£©øł¾ŻŅŌÉĻŹż¾Ż£¬ÄćČĻĪŖ¼×”¢ŅŅĮ½øö°ąÖŠÄÄøö°ąµÄѧɜ»ł“”ÖŖŹ¶±³ĖŠĒéæö½ĻŗĆ£æĒėĖµĆ÷ĄķÓÉ£ØŅ»ĢõĄķÓɼ“æÉ£©£»
£Ø3£©Čō¼×”¢ŅŅĮ½°ą×ÜČĖŹżĪŖ125£¬ĒŅ¶¼²Ī¼ÓĮĖ“Ė“Ī»ł“”ÖŖŹ¶¼ģ²ā£¬¹Ą¼Ę“Ė“Ī¼ģ²ā³É¼ØÓÅŠć£Øx”Ż95£©µÄѧɜČĖŹżŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
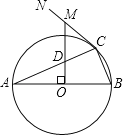
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćCĪŖ”ŃOÉĻŅ»µć£¬CNĪŖ”ŃOµÄĒŠĻߣ¬OM”ĶABÓŚµćO£¬·Ö±š½»AC”¢CNÓŚD”¢MĮ½µć£®
£Ø1£©ĒóÖ¤£ŗMD=MC£»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ5£¬AC=4![]() £¬ĒóMCµÄ³¤£®
£¬ĒóMCµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅ×ĪļĻßy£½x2+4x+3.
£Ø1£©Ēó³öøĆÅ×ĪļĻ߶Ō³ĘÖįŗĶ¶„µć×ų±ź£®
£Ø2£©ŌŚĖłøųµÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠÓĆĆčµć·Ø»³öÕāĢõÅ×ĪļĻߣ®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»øö²»ĶøĆ÷µÄæŚ“üÖŠÓŠ±źŗÅĪŖ1£¬2£¬3£¬4µÄĖÄøöŠ”Ēņ£¬³żŹż×Ö²»Ķ¬Ķā£¬Š”ĒņƻӊČĪŗĪĒų±š£¬ĆžĒņĒ°ĻČ½Į°č¾łŌČ£¬Ćæ“ĪĆžŅ»øöĒņ
(1)Ćž³öŅ»øöĒņ£¬Ćžµ½±źŗÅĪŖżŹżµÄøÅĀŹĪŖ .
(2)“Ó“üÖŠ²»·Å»ŲµŲĆžĮ½“Ī£¬ÓĆĮŠ±ķ»ņŹ÷דĶ¼Ēó³öĮ½Ēņ±źŗÅŹż×ÖĪŖŅ»ĘęŅ»Å¼µÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
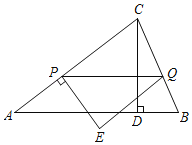
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£½5£¬CD”ĶABÓŚµćD£¬CD£½3£®µćP“ÓµćA³ö·¢ŃŲĻ߶ĪACŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÖÕµćCŌĖ¶Æ£®¹żµćP×÷PQ”ĪAB½»BCÓŚµćQ£¬¹żµćP×÷ACµÄ“¹Ļߣ¬¹żµćQ×÷ACµÄĘ½ŠŠĻߣ¬Į½Ļß½»ÓŚµćE£®ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©ĒóĻ߶ĪPQµÄ³¤£®£ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©
£Ø2£©µ±µćEĀäŌŚ±ßABÉĻŹ±£¬ĒótµÄÖµ£®
£Ø3£©µ±”÷PQEÓė”÷ACDÖŲµž²æ·ÖĶ¼ŠĪŹĒĖıߊĪŹ±£¬Ö±½ÓŠ“³ötµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com