
【题目】绝对值不大于3的所有整数有_____个.
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )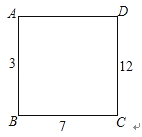
A.2
B.7
C.8
D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.
⑴ 如图1,若点D在BC边上(点D与B、C不重合),求∠BCE的度数.
⑵ 如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人按定期2年向银行储蓄,若年利率为3%(不计复利),到期支取时他活的利息为90元,则他存入的本金为( )
A. 3000 B. 2500 C. 1500 D. 1000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角? (填“是”或“不是”).
小丽经过三次折叠发现了∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,DC∥AB ,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=2时,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com