
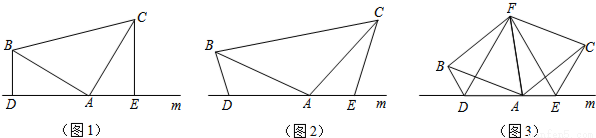
(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E. 证明:DE=BD+CE.
如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
(1)详见解析;(2)成立,理由详见解析;(3)△DEF是等边三角形.
【解析】
试题分析:(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)与(1)的证明方法一样;
(3)与前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.
试题解析:(1)证明: ∵BD⊥DE,CE⊥DE,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
∠BDA=∠CEA,∠ABD=∠CAE,AB=AC,
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
(2)【解析】
成立,证明如下:
∵∠BDA=∠AEC=∠BAC=a,
∴∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,
∴∠DBA=∠CAE,
在△ABD和△CAE中,
∠BDA=∠CEA,∠ABD=∠CAE,AB=AC,
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE.
△DEF为等边三角形,理由如下:
∵△ABF和△ACF均为等边三角形,
∴BF=AF=AB=AC=CF,
∠BAF=∠CAF=∠ABF=60°,
∴∠BDA=∠AEC=∠BAC=120°,
∴∠DBA+∠DAB=∠CAE+∠DAB=60°,
∴∠DBA=∠CAE.
在△BAD和△ACE中,
∠BDA=∠AEC,∠DBA=∠CAE,BA=AC,
∴△ADB≌△CEA(AAS),
∴BD=AE,∠DBA=∠CAE.
∵∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE.
在△BDF和△AEF中,
FB=FA,∠DBF=∠FAE,BD=AE,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
考点:1、全等三角形的判定和性质;2、等边三角形的判定.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知关于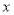 的一元二次方程
的一元二次方程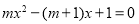 .
.
(1)求证:此方程总有两个实数根;
(2)若 为整数,当此方程的两个实数根都是整数时,求
为整数,当此方程的两个实数根都是整数时,求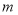 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,等边三角形ABC内接于⊙O,那么∠BOC的度数是( )

A.150° B.120° C.90° D.60°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市七年级上学期期末考试数学试卷(解析版) 题型:选择题
甲、乙、丙三辆车均在A、B两地间往返,三辆车在A、B两地间往返一次所需时间分别为5小时、3小时和2小时.现在三辆车同时在A地视为第一次汇合,甲车先出发,1 小时后乙车出发,再经过2小时后丙车出发.那么丙车出发( )小时后,三辆车第三次同时汇合于A地.
A.50 B.51 C.52 D.53
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市七年级上学期期末考试数学试卷(解析版) 题型:选择题
未来三年,我国将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿
用科学记数法表示为( ).
A.0.845×104亿元 B.8.45×103亿元
C.8.45×104亿元 D.84.5×102亿元
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省内江市八年级上学期期末考试数学试卷(解析版) 题型:解答题
(8分)先化简再求值:(x+3)²+(x+2)(x-2)-4x(x+3),其中x²+3x=2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省内江市八年级上学期期末考试数学试卷(解析版) 题型:选择题
若x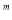 =9,x
=9,x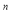 =6,x
=6,x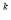 =4,则x
=4,则x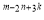 的值是( ).
的值是( ).
A.24 B.19 C.18 D.16
查看答案和解析>>
科目:初中数学 来源:2014-2015年江苏盐城建湖县城南实验初中八年级上12月月考数学卷(解析版) 题型:解答题
(本题满分6分)已知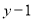 与
与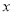 成正比例,当
成正比例,当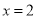 时,
时, .
.
(1)试求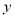 与
与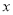 的函数关系式;
的函数关系式;
(2)求当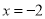 时,
时,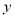 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏东台许河镇中学七年级上学期第二次月检数学试卷(解析版) 题型:选择题
下列说法错误的是( ).
A.长方体、正方体都是棱柱
B.六棱柱有六条侧棱、六个侧面
C.三棱柱的侧面是三角形
D.球体的三种视图均为同样的图形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com