练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在直角坐标系内，正方形如图摆放，已知顶点 A(a，0)，B(0，b) ，则顶点C的坐标为（ ）

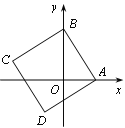
    A.(-b，a b)B.(-b，b - a)C.(-a，b - a)D.(b，b -a)

    【答案】B

    【解析】

    根据题意首先过点C作CE⊥y轴于点E，易得△AOB≌△BEC，然后由全等三角形的性质，证得CE=OB=b，BE=OA=a，继而分析求得答案．

    解：如图，过点C作CE⊥y轴于点E，

    ∵四边形ABCD是正方形，

    ∴AB=BC，∠ABC=90°，

    ∴∠ABO+∠CBE=90°，

    ∵∠ABO+∠BAO=90°，

    ∴∠CBE=∠BAO，

    在△ABO和△BCE中，

    ∴△AOB≌△BEC（AAS），

    ∴BE=OA=a，CE=OB=b，

    ∴OE=OB-BE=b-a，

    ∴顶点C的坐标为：（-b，b-a）．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商场用2700元购进甲、乙两种商品共100件，这两种商品的进价、标价如下表所示：

    甲种

    乙种

    进价（元/件）

    15

    35

    标价（元/件）

    20

    45

    （1）求购进两种商品各多少件？

    （2）商品将两种商品全部卖出后，获得的利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对代数式，老师要求任意取一个x的值后求出代数式的值．圆圆发现，大家所求得的代数式的值都大于等于0，即x＝－3时代数式的最小值是0．利用这个发现，圆圆试着写出另外一些结论：①在x＝－3时，代数式(x＋3)2＋2的最小值为2；②在a＝－b时，代数式(a＋b)2＋m的最小值为m；③在c＝－d时，代数式－(c＋d)2＋n的最大值为n；④在时，代数式的最大值为29．其中正确的为（ ）

    A. ①②③B. ①③C. ①④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，AC= ，BC=1，D在AC上，将△ADB沿直线BD翻折后，点A落在点E处，如果AD⊥ED，那么△ABE的面积是（ ）

    A.1
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）（阅读理解）

    如图（1），AD是△ABC的中线，作△ABC的高AH．

    ∵AD是△ABC的中线

    ∴BD＝CD

    ∵S△ABD＝BDAH，S△ACD＝CDAH

    ∴S△ABD　 　S△ACD（填：＜或＞或＝）

    （2）（结论拓展）

    △ABC中，D是BC边上一点，若，则＝　 　

    （3）（结论应用）

    如图（3），请你将△ABC分成4个面积相等的三角形（画出分割线即可）

    如图（4），BE是△ABC的中线，F是AB边上一点，连接CF交BE于点O，若，则＝　 　．说明你的理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB＝BC＝1，CD＝，DA＝1，且∠B＝90°．求：

    （1）∠DAC的度数；

    （2）四边形ABCD的面积（结果保留根号）；

    （3）将△ABC沿AC翻折至△AB′C，如图所示，连接B′D，求△AB′D的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】操作：在△ABC中，AC=BC=2，∠C=90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．图1，2，3是旋转三角板得到的图形中的3种情况．
    研究：

    （1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系，并结合图2加以证明；
    （2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由；
    （3）若将三角板的直角顶点放在斜边AB上的M处，且AM：MB=1：3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合图4加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下：12：00时是一个两位数,数字之和为7；13：00时十位与个位数字与12：00是所看到的正好互换了；14：00时比12：00时看到的两位数中间多出一个0.如果设小明在12：00看到的数的十位数字是x，个位数字是y，根据题意可列方程组为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在半径为6cm的⊙O中，点A是劣弧 的中点，点D是优弧 上一点，且∠D=30下列四个结论：①OA⊥BC；②BC= cm；③cos∠AOB= ；④四边形ABOC是菱形.其中正确结论的序号是（ ）

    A.①③
    B.①②③④
    C.①②④
    D.②③④

    查看答案和解析>>

    同步练习册答案