
【题目】如图,在平面直角坐标系中,直线AB:y=kx+4(k≠0)与x轴,y轴,交于A、B两点,点C是BO的中点且tan∠ABO=![]()
(1)求直线AC的解析式;
(2)若点M是直线AC的一点,当![]() 时,求点M的坐标.
时,求点M的坐标.
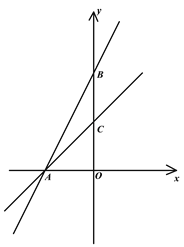
【答案】(1)y=x+2(2)M(-6,-4),(2,4)
【解析】分析:(1)在Rt△ABO中求出OA的长,由点A,C的坐标即可求AC的解析式;(2)设M(m,m+2),则S△ABM=![]() ×|m-(-2)|BC,S△AOC=2,列方程求m.
×|m-(-2)|BC,S△AOC=2,列方程求m.
详解:(1)根据题意得,OB=4,又tan∠ABO=![]() ,
,
所以OA=2,则A(-2,0).
因为点C是BO的中点,所以OC=2,则C(0,2).
所以直线AC的解析式为y=x+2.
(2)设M(m,m+2),
因为S△AOC=2,S△ABM=![]() ×|m-(-2)|BC,
×|m-(-2)|BC,
所以![]() ×2|m-(-2)|=2×2,解得m=-6或m=2,
×2|m-(-2)|=2×2,解得m=-6或m=2,
当m=-6时,m+2=-4;
当m=2时,m+2=4.
所以M的坐标为(-6,-4),(2,4).


科目:初中数学 来源: 题型:
【题目】同学报名次参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示)
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率P为___________;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1,利用列表法或树状图加以说明;
(3)该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,点
,点![]() 是斜边
是斜边![]() 上的中点,过点
上的中点,过点![]() 作
作![]() 边上的垂线
边上的垂线![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
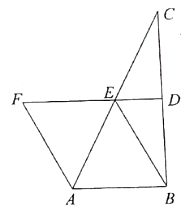
(1)找出图中与![]() 相等的所有线段.
相等的所有线段.
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数![]() 都可以写成两个正整数相乘的形式,我们把两个乘数的差的绝对值最小的一种分解
都可以写成两个正整数相乘的形式,我们把两个乘数的差的绝对值最小的一种分解![]() 称为正整数
称为正整数![]() 的最佳分解,并定义一个新运算
的最佳分解,并定义一个新运算![]() .例如:12=1×12=2×6=3×4,则
.例如:12=1×12=2×6=3×4,则![]() .那么以下结论中:①F(2)=
.那么以下结论中:①F(2)=![]() ;②F(24)=
;②F(24)=![]() ;③若
;③若![]() 是一个完全平方效,则
是一个完全平方效,则![]() ;④若
;④若![]() 是一个完全立方数(即
是一个完全立方数(即![]() ,
,![]() 是正整数),则
是正整数),则![]() .正确的个数为( )
.正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
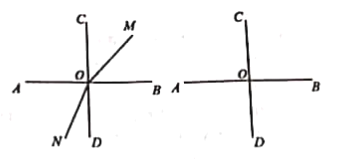
【题目】如图,两条直线AB,CD相交于点O,且![]() ,射线OM从OB开始绕O点逆时针方向旋转,速度为
,射线OM从OB开始绕O点逆时针方向旋转,速度为![]() ,射线ON同时从OD开始绕O点顺时针方向旋转,速度为
,射线ON同时从OD开始绕O点顺时针方向旋转,速度为![]() .两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
(1)当![]() 时,若
时,若![]() .试求出的值;
.试求出的值;
(2)当![]() 时,探究
时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
查看答案和解析>>
科目:初中数学 来源: 题型:
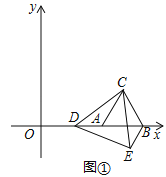
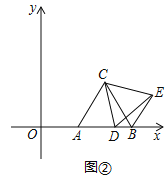
【题目】如图①,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(5,0),(9,0),点D是x轴正半轴上一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.
(Ⅰ)直接写出点C的坐标,并判断△CDE的形状,说明理由;
(Ⅱ)如图②,当点D在线段AB上运动时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长及此时点D的坐标;若不存在,说明理由;
(Ⅲ)当△BDE是直角三角形时,求点D的坐标.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
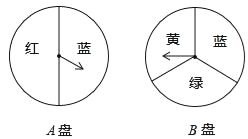
A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com