
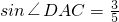 ,AE、DE的长是方程x2-140x+k=0的两根.
,AE、DE的长是方程x2-140x+k=0的两根. 形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.
形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.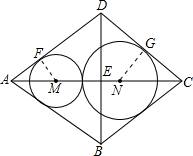 解:(1)∵ABCD是菱形
解:(1)∵ABCD是菱形
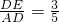
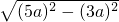 =4a
=4a =
=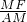
 t
t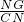 =
=
 NG
NG t+NG
t+NG t+NG+
t+NG+ NG=160
NG=160 t
t t)2
t)2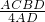 =48(mm)
=48(mm)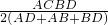 =30(mm).
=30(mm). ,可以求出DE的长,再根据根与系数的关系即可求得DE的长度;
,可以求出DE的长,再根据根与系数的关系即可求得DE的长度;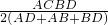 =30(mm),所以可以加工直径为60mm的圆形零件2个;所以加工直径为48mm的圆形零件,最能充分利用这块材料.
=30(mm),所以可以加工直径为60mm的圆形零件2个;所以加工直径为48mm的圆形零件,最能充分利用这块材料.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
| 3 | 5 |
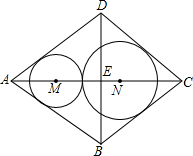 形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.
形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.查看答案和解析>>
科目:初中数学 来源:2001年浙江省衢州市中考数学试卷(解析版) 题型:解答题
 ,AE、DE的长是方程x2-140x+k=0的两根.
,AE、DE的长是方程x2-140x+k=0的两根.
查看答案和解析>>
科目:初中数学 来源:2001年浙江省金华市中考数学试卷(解析版) 题型:解答题
 ,AE、DE的长是方程x2-140x+k=0的两根.
,AE、DE的长是方程x2-140x+k=0的两根.
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《四边形》(02)(解析版) 题型:解答题
 ,AE、DE的长是方程x2-140x+k=0的两根.
,AE、DE的长是方程x2-140x+k=0的两根.
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题
 ,AE、DE的长是方程x2-140x+k=0的两根.
,AE、DE的长是方程x2-140x+k=0的两根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com